
本文为《最优化:建模、算法与理论》8.6 交替方向乘子法 对应的代码及其说明代码作者:文再文、刘浩洋、户将为方便阅读将代码注释中
本文为《最优化:建模、算法与理论》8.6 交替方向乘子法 对应的代码及其说明
代码作者:文再文、刘浩洋、户将
为方便阅读将代码注释中的latex写出来了
利用 ADMM 求解 LASSO 问题的原问题
针对 LASSO 问题

引入拉格朗日乘子 

在 ADMM 的每一步迭代中,交替更新 


%% 初始化和迭代准备
% 函数通过优化上面给出的增广拉格朗日函数,以得到 LASSO 问题的解.
% 输入信息: 



% 输出信息: 迭代得到的解 
% * |out.fvec| :每一步迭代的 LASSO 问题目标函数值
% * |out.fval| :迭代终止时的 LASSO 问题目标函数值
% * |out.tt| :运行时间
% * |out.itr| :迭代次数
% * |out.y| :迭代终止时的对偶变量 
% * |out.nrmC| :约束违反度,在一定程度上反映收敛性
function [x, out] = LASSO_admm_primal(x0, A, b, mu, opts)
%%%
% 从输入的结构体 |opts| 中读取参数或采取默认参数.
% * |opts.maxit| :最大迭代次数
% * |opts.ftol| :针对函数值的停机准则,当相邻两次迭代函数值之差小于该值时认为该条件满足
% * |opts.gtol| :针对 
% * |opts.sigma| :增广拉格朗日系数
% * |opts.gamma| : 
% * |opts.verbose| :不为 0 时输出每步迭代信息,否则不输出
if ~isfield(opts, 'maxit'); opts.maxit = 5000; endnif ~isfield(opts, 'sigma'); opts.sigma = 0.01; endnif ~isfield(opts, 'ftol'); opts.ftol = 1e-8; endnif ~isfield(opts, 'gtol'); opts.gtol = 1e-14; endnif ~isfield(opts, 'gamma'); opts.gamma = 1.618; endnif ~isfield(opts, 'verbose'); opts.verbose = 1; end
%%%
% 迭代准备
k = 0;ntt = tic;nx = x0;nout = struct();
%%%
% 初始化 ADMM 的辅助变量 


[m, n] = size(A);nsm = opts.sigma;ny = zeros(n,1);nz = zeros(n,1);
%%%
% 计算并记录起始点的目标函数值。
fp = inf; nrmC = inf;nf = Func(A, b, mu, x);nf0 = f;nout.fvec = f0;
%%%
% Cholesky 分解, 

AtA = A'*A;nR = chol(AtA + opts.sigma*eye(n));nAtb = A'*b;
%% 迭代主循环
% 迭代主循环,当 (1) 达到最大迭代次数或 (2) 目标函数的变化小于阈值或 (3) 自变量 
while k < opts.maxit && abs(f - fp) > opts.ftol && nrmC > opts.gtoln fp = f;
%%%
% 更新 

% 
w = Atb + sm*z - y;n x = R (R' w);
%%%
% 更新 

% 即 
c = x + y/sm;n z = prox(c,mu/sm);
%%%
% 以 


% 更新 

% 以 
y = y + opts.gamma * sm * (x - z);n f = Func(A, b, mu, x);n nrmC = norm(x-z,2);
%%%
% 输出每步迭代的信息. 迭代步 
if opts.verbosen fprintf('itr: %4dtfval: %etfeasi:%.1en', k, f,nrmC);n endn k = k + 1;n out.fvec = [out.fvec; f];nend
%%%
% 退出循环,记录输出信息。
out.y = y;nout.fval = f;nout.itr = k;nout.tt = toc(tt);nout.nrmC = norm(c - y, inf);nend
%% 辅助函数
%%%
% 函数 

function y = prox(x, mu)ny = max(abs(x) - mu, 0);ny = sign(x) .* y;nend
%%%
% LASSO 问题的目标函数 
function f = Func(A, b, mu, x)nw = A * x - b;nf = 0.5 * (w' * w) + mu*norm(x, 1);nend
利用 ADMM 求解 LASSO 对偶问题
针对 LASSO 问题

考虑其对偶问题的 ADMM 等价形式

引入 

在 ADMM 的每一步迭代中,交替更新 



%% 初始化和迭代准备
% 函数通过优化上面给出的增广拉格朗日函数,以得到 LASSO 问题的解。
% 输入信息: 



% 输出信息: 迭代得到的解 
% * |out.fvec| :每一步迭代的 LASSO 问题目标函数值
% * |out.fval| :迭代终止时的 LASSO 问题目标函数值
% * |out.tt| :运行时间
% * |out.itr| :迭代次数
% * |out.y| :迭代终止时的对偶变量 
% * |out.nrmC| :迭代终止时的约束违反度,在一定程度上反映收敛性
function [x, out] = LASSO_admm_dual(x0, A, b, mu, opts)
%%%
% 从输入的结构体 |opts| 中读取参数或采取默认参数。
% * |opts.maxit| :最大迭代次数
% * |opts.ftol| :针对函数值的停机准则,当相邻两次迭代函数值之差小于该值时认为该条件满足
% * |opts.gtol| :针对 
% * |opts.sigma| :增广拉格朗日系数
% * |opts.gamma| : 
% * |opts.verbose| :不为 0 时输出每步迭代信息,否则不输出
if ~isfield(opts, 'maxit'); opts.maxit = 5000; endnif ~isfield(opts, 'sigma'); opts.sigma = 0.5; endnif ~isfield(opts, 'ftol'); opts.ftol = 1e-8; endnif ~isfield(opts, 'gtol'); opts.gtol = 1e-6; endnif ~isfield(opts, 'gamma'); opts.gamma = 1.618; endnif ~isfield(opts, 'verbose'); opts.verbose = 1; end
%%%
% 迭代准备。
tt = tic;nk = 0;nx = x0;nout = struct();
%%%
% 初始化对偶问题的对偶变量 
[m, ~] = size(A);nsm = opts.sigma;ny = zeros(m,1);
%%%
% 记录在初始时刻原问题目标函数值。
f = .5*norm(A*x - b,2)^2 + mu*norm(x,1);nfp = inf;nout.fvec = f;nnrmC = inf;
%%%
% Cholesky 分解, 

% 与原始问题同样的,由于罚因子在算法的迭代过程中未变化,事先缓存 Cholesky 分解可以加速迭代过程。
W = eye(m) + sm * (A * A');nR = chol(W);
%% 迭代主循环
% 迭代主循环,当 (1) 达到最大迭代次数或 (2) 目标函数的变化小于阈值或
% (3) 自变量 
while k < opts.maxit && abs(f - fp) > opts.ftol && nrmC > opts.gtoln fp = f;
%%%
% 对 

z = proj( - A' * y + x / sm, mu);
%%%
% 针对 

% 这里同样利用了事先缓存的 Cholesky 分解来加速 
h = A * (- z*sm + x) - b;n y = R (R' h);
%%%
% 令 
% 增广拉格朗日函数对 

% 针对 

% 利用 |nrmC| (约束违反度的范数)作为停机判断依据。
c = z + A' * y;n x = x - opts.gamma * sm * c;n nrmC = norm(c,2);
%%%
% 计算更新后的目标函数值,记录在 |out.fvec| 中。当 |opts.verbose| 不为 0 时输出详细的迭代信息。
f = .5*norm(A*x - b,2)^2 + mu*norm(x,1);n if opts.verbosen fprintf('itr: %4dtfval: %etfeasi: %.1en', k, f, nrmC);n endn k = k + 1;n out.fvec = [out.fvec; f];nend
%%%
% 记录输出信息。
out.y = y;nout.fval = f;nout.itr = k;nout.tt = toc(tt);nout.nrmC = nrmC;nend
%% 辅助函数
% 到无穷范数球 
function w = proj(x, t)nw = min(t, max(x, -t));nend
考虑LASSO问题:

首先考虑利用 ADMM 求解原问题:将其转化为 ADMM 标准问题

则可以利用 ADMM 求解. 相应的,对于 LASSO 对偶问题

则等价于

对于上述的两个等价问题利用 ADMM 求解.
%% 构造 LASSO 问题
% 设定随机种子.
clear;nseed = 97006855;nss = RandStream('mt19937ar','Seed',seed);nRandStream.setGlobalStream(ss);
%%%
% 构造 LASSO 优化问题
% 
% 生成随机的矩阵 



m = 512;nn = 1024;nA = randn(m, n);nu = sprandn(n, 1, 0.1);nb = A * u;nx0 = randn(n, 1);nmu = 1e-3;
%% 利用 ADMM 求解 LASSO 问题
% 首先在更严格的停机准则下进行试验,将收敛时得到的历史最优函数值作为真实的最优值的参考 
opts = struct();nopts.verbose = 0;nopts.maxit = 2000;nopts.sigma = 1e-2;nopts.ftol = 1e-12; nopts.gtol = 1e-15;n[x, out] = LASSO_admm_primal(x0, A, b, mu, opts);nf_star = min(out.fvec);
%%%
% 利用 ADMM 求解 LASSO 对偶问题.
opts = struct();nopts.verbose = 0;nopts.maxit = 2000;nopts.sigma = 1e2;nopts.ftol = 1e-8; nopts.gtol = 1e-10;n[x, out] = LASSO_admm_dual(x0, A, b, mu, opts);ndata1 = (out.fvec - f_star)/f_star;nk1 = length(data1);
%%%
% 利用 ADMM 求解 LASSO 原问题.
opts = struct();nopts.verbose = 0;nopts.maxit = 2000;nopts.sigma = 1e-2;nopts.ftol = 1e-8; nopts.gtol = 1e-10;n[x, out] = LASSO_admm_primal(x0, A, b, mu, opts);ndata2 = (out.fvec - f_star)/f_star;nk2 = length(data2);
%% 结果可视化
% 对每一步的目标函数值与最优函数值的相对误差进行可视化.
fig = figure;nsemilogy(0:k1-1, data1, '-', 'Color',[0.2 0.1 0.99], 'LineWidth',2);nhold onnsemilogy(0:k2-1, data2, '-.','Color',[0.99 0.1 0.2], 'LineWidth',1.5);nlegend('ADMM解对偶问题','ADMM解原问题');nylabel('$(f(x^k) - f^*)/f^*$', 'fontsize', 14, 'interpreter', 'latex');nxlabel('迭代步');nprint(fig, '-depsc','admm.eps');
结果分析
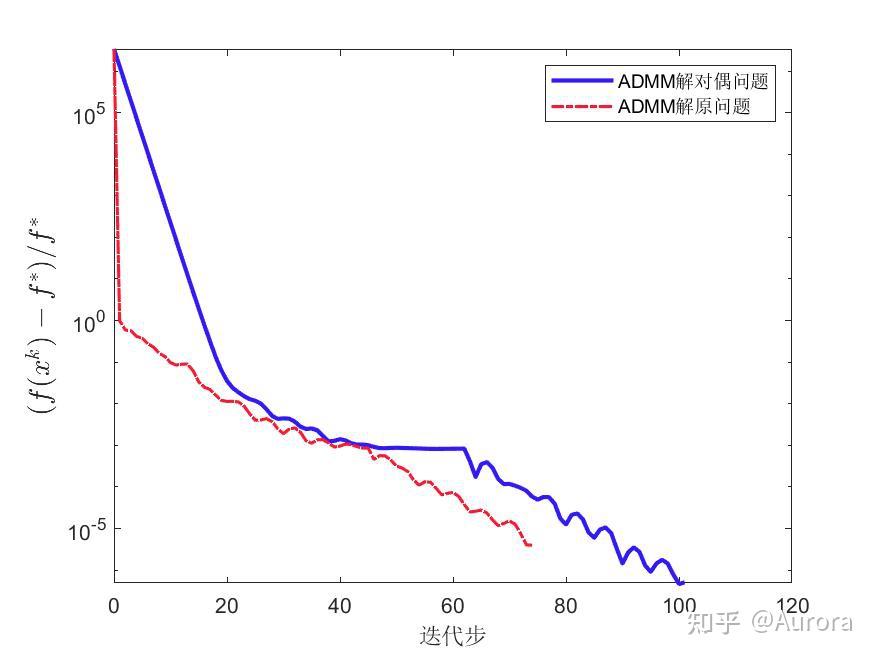
上图反映了使用 ADMM 求解 LASSO 原问题和对偶问题的表现。在两个问题上目标函数值都存在波动,表明 ADMM 并非下降算法,然而在没有使用连续化策略的情况下,ADMM 依然达到了收敛,这说明 ADMM 较之其它算法具有一定的优越性。注意,虽然在这一例子中 ADMM求解原问题所需迭代次数较少,但求解对偶问题时每一步迭代时间更短。综合看来在该例子中 ADMM 求解对偶问题的性能更高。









