综合能源系统多时刻优化模型建立与求解
1. 多时刻优化的定义在之前的专栏中,我们已经完整的建立了热电型综合能源系统的模型并通过gurobi实现了求解。上述模型可以认为是
1. 多时刻优化的定义
在之前的专栏中,我们已经完整的建立了热电型综合能源系统的模型并通过gurobi实现了求解。上述模型可以认为是最为基本的版本,有很多很多改进空间,如从单时刻优化变为多时刻优化、增加储能模型、增加管网/建筑蓄热、考虑需求侧响应、从集中式求解变为分布式求解、增加光伏风电等新能源等等。许多SCI论文也都是以模型、算法的组合式改进为创新点进行发表的。本文将针对多时刻优化这一经典问题,对之前的基本模型进行改进。首先声明一下:本文的观点并不一定是完全正确的,代码也一定不是最简洁、最易懂的,本文旨在提供一个基本思路,供初学者入门。
多时刻优化和单时刻优化的主要区别是:单时刻优化仅仅以当前时刻的指标(如经济成本、系统能耗等)为优化目标,而多时刻优化以未来一段时间的指标之和为优化目标。这是一个典型的模型预测控制问题,如下图所示:
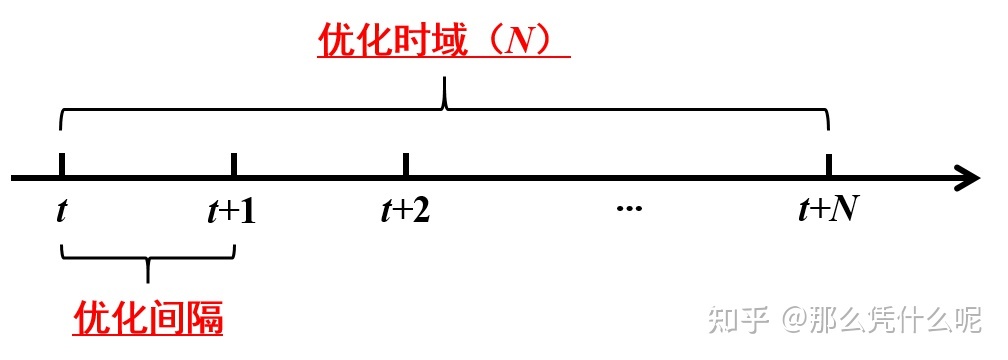
其中,优化间隔(optimization interval)一般为1h、15min等,由于一般是对未来一天进行调度,因此对应的优化时域(optimization horizon)往往分别为24、96等。
2. 多时刻优化下的建模
相比于单时刻优化,多时刻优化建模无非需要多考虑两点:
- 如何快速表示多时刻下的目标函数和约束条件。以间隔为1h、时域为24的多时刻优化问题为例,目标函数(这里指经济成本等指标的加和)和约束条件都将变为单时刻优化的24倍,如果要一个一个手动生成是不现实的。解决这个问题的基本思路就是巧用for循环来让程序自动生成目标函数和约束条件。
- 如何处理时序相关的约束条件。以储能系统为例(后续会讲到具体模型,但基本原理并不难懂),t+1时刻的状态(蓄能量)总是取决于t时刻的状态。处理这类时序相关的约束条件,关键是处理好其初始态和中间态的不同表达形式。
和时序相关的约束条件有很多,此处介绍三类最常考虑的时序约束条件:
- 机组爬坡率(unit ramping rate):一般地,产能机组在一段时间内(如热电联产机组、锅炉、冷机等)的产能量变化是有限的,而非能从0%变化到100%。例如,热电联产机组的变化率(又称为爬坡率)为0.5%-1.5%/min。这表示t+1时刻的机组产能量取决于t时刻的机组产能量。以之前专栏中的燃气锅炉模型为例,机组爬坡率约束表示如下:






- 热力管网传输时延(transmission delay):相比于电力网络,热力管网的传输介质(水)传输速度很慢,对于长距离输运管道存在明显传输时延的现象。因此,t+1时刻的管道出口温度往往取决于t时刻甚至更早时刻的管网入口温度。其约束形式(基于简化节点法)已经在这篇专栏中讲过(专栏中的
等同于本篇文章中的t,都表示某时刻,之后统一用t表示),此处不再赘述。本文采用基于Lax-Wendroff方法的热力管网传输时延约束,该模型的优点在于它假设当前时刻的状态只和上一时刻的状态有关,这样能够简化时序约束的建立过程,其数学表示形式如下:
式中, 








- 储能设备SOC(State of charging):储能设备能够在能源价格处于低谷时进行储能,并在电价高或用能高峰期释能,不仅能够削峰填谷,还能够提高经济性、促进可再生能源消纳等。常见的储能系统包含蓄电系统(Electrical energy storage,EES)、蓄热系统(Thermal energy storage,TES)等。以EES为例,其储能模型可以表示为以下形式:













3. 多时刻优化下的编程
3.1 优化变量设置
在多时刻优化下,优化变量做如下定义:
# 以热力管网节点的供水温度为例:n# period为优化时域,n_node为节点个数nts = m.addVars(period, n_node, lb=lb_ts, ub=ub_ts, name='node supply temp')
每个优化变量在单时刻优化的基础上增加了一个维度,即时间维度。可以把这个变量看作一个period行、n_node列的数组,每一行都包含了某个时刻下各个节点的供水温度变量。在调用其中的某个变量时,可以采用如下方式调用:
# 调用ts第1行、第1列的变量nts_0_0 = ts[0, 0]
3.2 添加机组爬坡率约束
先从最简单的说起,仍以锅炉热出力为例,机组爬坡率约束可以如下添加:
h_gb = m.addVars(period, lb=lb_gb, ub=ub_gb, name='gas boiler heating output')nm.addConstrs(h_gb1[t+1] - h_gb1[t] <= r_u_gb1 * interval for t in range(period - 1)) # interval为优化间隔nm.addConstrs(h_gb1[0] - h_gb1_init <= r_u_gb1 * interval)nm.addConstrs(h_gb1[t+1] - h_gb1[t] >= -r_d_gb1 * interval for t in range(period - 1))nm.addConstrs(h_gb1[0] - h_gb1_init >= -r_d_gb1 * interval)
这段代码很好理解,关键在于需要单独处理初始条件(line 3和5)。t=0时刻的锅炉热出力要取决于整个系统初始态下的锅炉热出力h_gb1_init。时序相关的约束条件都存在这个问题,也可以统一采用这种方法进行处理。注意:为使行文简单,后续均不再单独列出初始态下的约束条件。
3.3 添加储能设备SOC约束
储能SOC约束并不难添加,不过巧设变量可以降低编程难度。一般地,通常设置蓄能量 

p_ch = m.addVars(period, lb=lb_ch, ub=ub_ch, name='ees charging energy')np_dch = m.addVars(period, lb=lb_dch, ub=ub_dch, name='ees discharging energy')nsoc = m.addVars(period, lb=lb_soc, ub=ub_soc, name='ees soc')nm.addConstrs(p_ch[t] * p_dch[t] == 0 for t in range(period))nm.addConstrs(soc[t+1] == soc[t] * eta_loss + interval / cap_ees * (p_ch * eta_ch - p_dch * eta_dch) n for t in range(period - 1))
可以看到,通过添加SOC优化变量,约束条件写起来就很容易。
3.4 添加热力管网传输时延约束
从模型来看,热力管网传输时延约束就是一个等式约束,但是糅合了节点温度混合和温度耗散后,编程会变得非常复杂。以供水管网为例(回水管网和供水管网基本完全相同),各类温度如图所示:
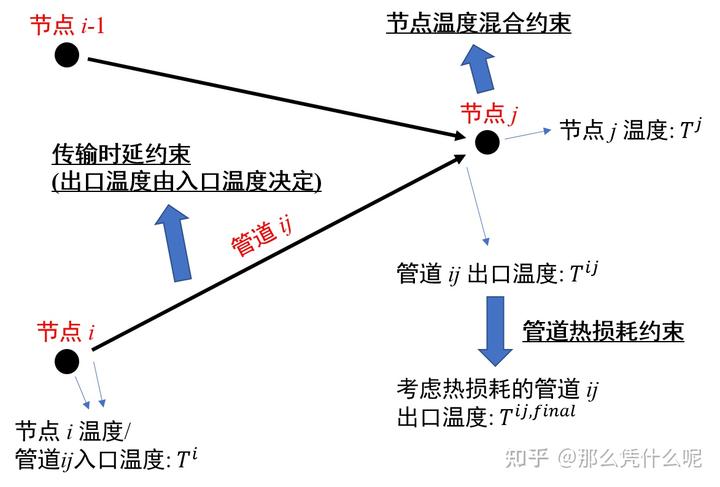
从中可以看出,温度可以分为三类:一是节点温度,它同时也是其出水管道(即从水从该管道流出)的入口温度;二是管道的出口温度,该温度由(历史时刻的)管道入口温度决定;三是考虑了热损耗效应的管道实际出口温度。通过定义这三类温度,就能够很容易清楚管道传输时延约束、节点温度混合约束和管道热损耗约束都表示了什么。以供水管网为例,主要代码如下:
# 节点温度nts = m.addVars(period, n_node, lb=lb_ts, ub=ub_ts, name='node supply temp')n# 管道出口温度nts_pipe = m.addVars(period, n_node, n_node lb=lb_ts, ub=ub_ts, name='pipe outlet temp')n# 考虑热损耗后的管道出口温度nts_pipe_final = m.addVars(period, n_node, n_node lb=lb_ts, ub=ub_ts, name='pipe outlet temp after loss')nfor t in range(period):n for i in range(n_node):n # 节点温度混合约束n # X_hn_sup为之前专栏中建立的描述热力管网拓扑的数组,可见之前公开的源代码。[0]表示管道流量n m.addConstr(quicksum(X_hn_sup[j][i][0] * ts_pipe_final[t, j, i] for j in range(n_node)) ==n quicksum(X_hn_sup[j][i][0] for j in range(n_node)) * ts[t, i])n for j in range(n_node):n # 若节点i和节点j之间存在管道连接,则添加管道热损耗约束和传输时延约束n if X_hn_sup[i][j][0] != 0:n # 添加管道热损耗约束n # t_amb为环境温度数组,X_hn_sup中的[1]表示热损耗中指数的那一坨(便于表示)n m.addConstr(ts_pipe_final[t, i, j] == (ts_pipe[t, i, j] - t_amb[t]) * X_hn_sup[i][j][1] + t_amb[t])n # 添加管道传输时延约束n # X_hn_sup中的[2]和[3]分别表示式中的那两坨,同上,都是为了方便表示n m.addConstr((ts_pipe[t+1, i, j] + ts[t+1, i] - ts_pipe[t, i, j] - ts[t, i] + n X_hn_sup[i][j][2] * (ts_pipe[t+1, i, j] + ts_pipe[t, i, j] - ts[t+1, i] - ts[t, i]) n + X_hn_sup[i][j][3] * (ts_pipe[t+1, i, j] + ts_pipe[t, i, j] + ts[t+1, i] + ts[t, i] n - 4 * t_amb[t])) * X_hn_sup[i][j][0] == 0)
3.5 添加目标函数
目标函数非常简单,只需要按照上述写法,用quicksum函数进行累加即可。综上,我们就较为完整地实现了综合能源系统多时刻优化调度的编程,并且新增加了三类典型的时序相关约束,包括机组爬坡约束、储能约束和热力管网传输时延约束。临近春节,没有时间和精力将之前专栏中的case进行相应的修改,如果有问题欢迎在评论区或私信交流。










