1stOpt 新特性

当前时间：2020年10月18日1stOpt9.0 新特性七维高科公司今天发布了1stOpt9.0版本新特性，软件得12月1日才能升级。简单说一下更新内容

当前时间：2020年10月18日

1stOpt9.0 新特性

七维高科公司今天发布了1stOpt9.0版本新特性，软件得12月1日才能升级。简单说一下更新内容。

• 1. 多层自回归网络工具箱升级

增加了“多模”模型结构，对拟合及分类在效果方面有大幅提高，尤其对低维数据，同时支持单一输入。

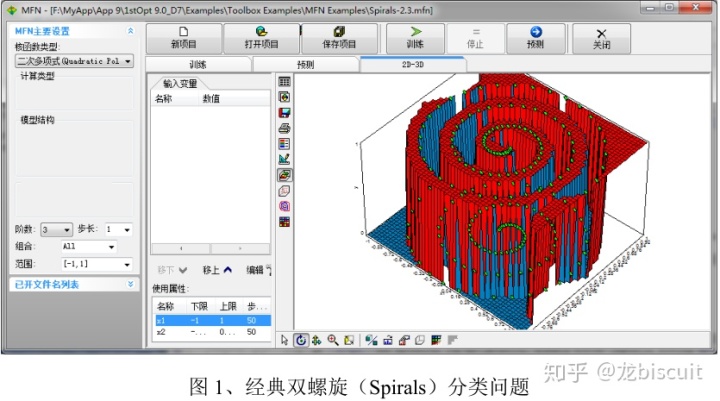
自己没用这个解决过实际问题，没啥发言权，就不乱说了。

但所有工具箱几乎都用到1stOpt电子表格，就说说电子表格吧。以前用神经网络工具箱算过大的数据集，感觉1stOpt电子表格行数太多了比较卡。比如用传感器收集振动碾振动加速度，采样频率10000Hz，那就是每秒采集10000个数，采集半小时就是18000000个数，8个传感器就是18000000*8个数据，这还只是自变量，可想数据量有多大。用matlab自带的神经网络工具箱，这个数据量放在8个mat里还是没问题的，也还能算，比较慢就是了。但把这些数据一股脑放入1stOpt8.0的电子表格里是不行的，会直接卡死的。1stOpt9.0版本可以直接读入matlab的mat数据文档：

这方面应该是做了优化吧。当今，不少问题都和大数据沾些边，所以如果这方面有改进，那就太实用了。

• 2.增加了线性 、 多项式及完全多项式拟合计算功能

用matlab2016b的拟合工具箱可以发现，其对于多项式拟合速度非常快，数据量很大时依然如此（缺点是自定义函数只能有三个自变量）。1stOpt可以很方便的自定义任意多自变量的函数，非线性拟合功能也很强，但对于大数据量的线性或多项式拟合速度较慢，有时效果也不太好（我以前试过大数据量的傅里叶级数拟合，非线性也较慢，其实只要大数据量问题都不会很快）。9.0版本对于线性、多项式及完全多项式这块增加了新的函数用以应对大数据量（主要自变量多）的问题：

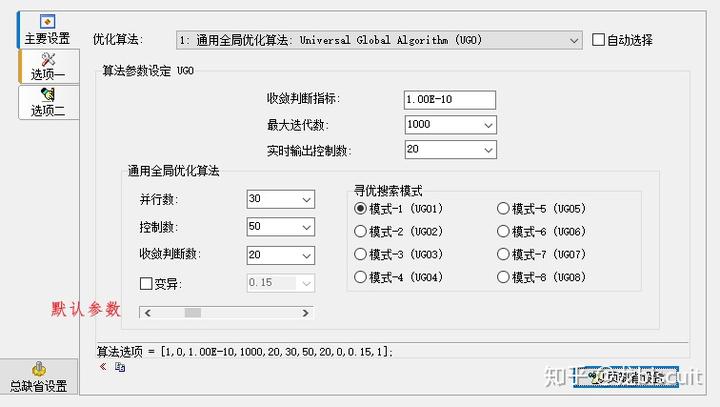
• 3. 对于某些非线性问题 参数赋予为 初值为 0 时 时 效率大 幅 提高

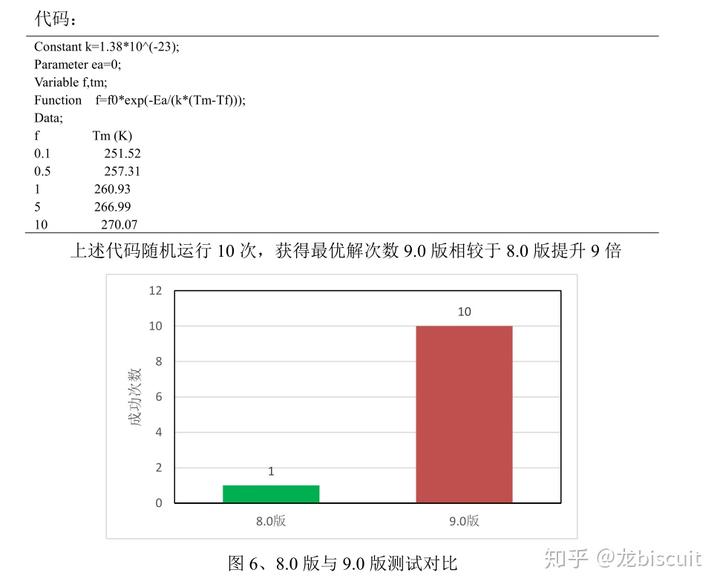
8.0版本把默认参数调大些，也能算的不错，但也不能保证百分之百能算好，肯定比9.0还慢些：

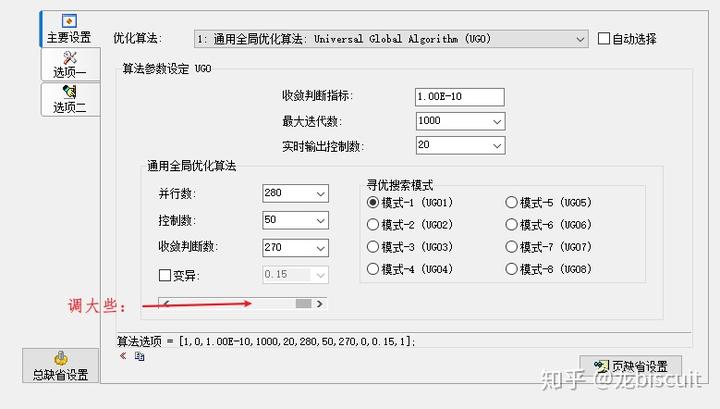
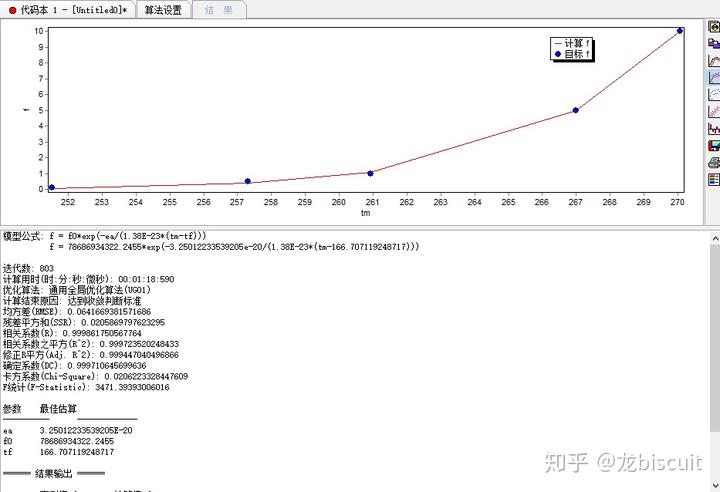
• 4. 目标函数可以选择

拟合 时目标函数 可 选择最小二乘（ 实际 输出值及对应计算值差值平方和最小）或数 确定系数 DC（ （应 对应 WeightedReg = 3 命令为 ，也即权重系数为 w =Variance^2） ） ， 对于多数据多输出且 输出 值数量级相差 很大时，选择后者可兼顾整体，效果更好

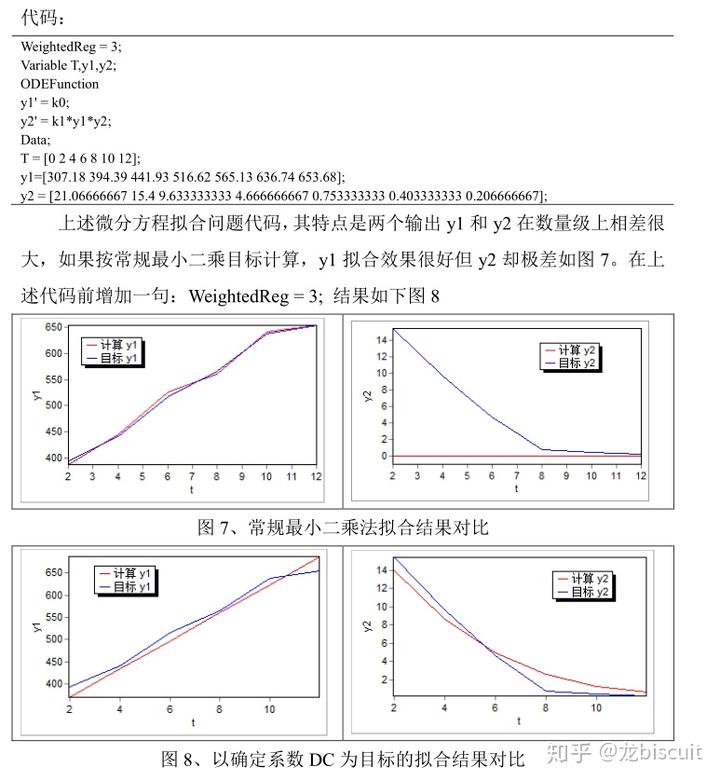
其实就是吧目标函数的最小二乘归一化了（以 sum(((y-y')/y')^2) 为目标函数）。这个关键字8.0版本就有了啊，但不知道8.0为什么不好使。

• 5. 输出结果多页面保存，多页面预测

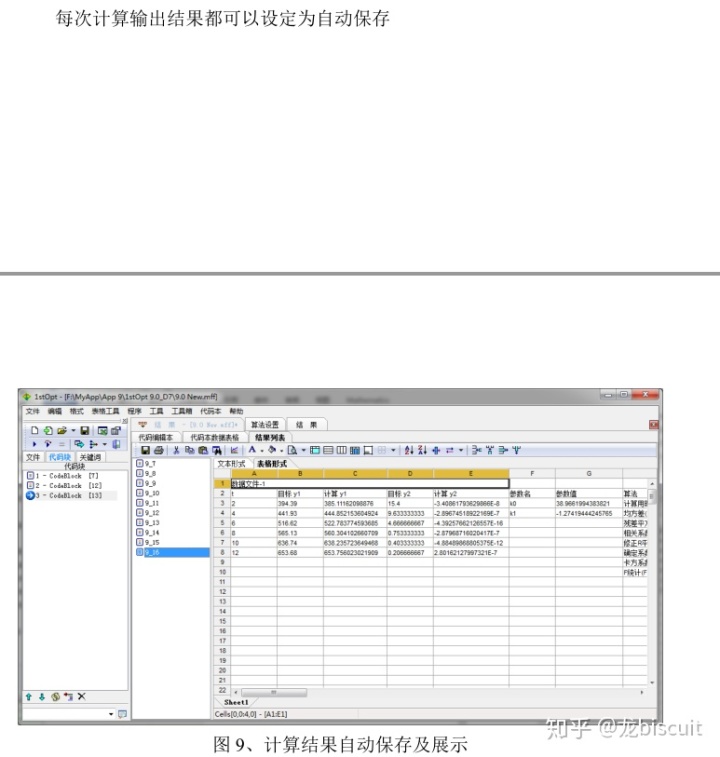
另外，计算的结果数据和图片可以同时保存：

在8.0版本中计算结果的图片得一个一个手动保存。

这些功能超级实用，点赞，再也不用一个一个的来保存了!

• 6. 调用的 外部高级语言编写的 dll 目标函数时支持 循环 常数（LoopConstan） ） 传递 ，同时也支持数据直接从代码本传入目标函数动态库

如果需要循环计算但目标函数太复杂，想用dll计算目标函数，在8.0企业版本就搞不定了，因为不知道当前循环到哪些常数了。当然8.0的开发版肯定可以，方法是用matlab或别的什么语言调用开发版或其api就行，循环常数在matlab或其他语言中进行，8.0的1stOpt就是个优化器，多次调用就是了。9.0可以将循环常数和Data数据传入dll中，对于有些问题也不用fortran读入文本文档了（我还写了一篇文章如何用dll计算时提高计算效率：https://zhuanlan.zhihu.com/p/264988656）

龙biscuit：1stopt调用fortran90的dll时只读入一次文本进而加快计算速度

很多需要使用dll的批量优化问题在9.0版本中很容易就可以解决了：

• 7. 还有几个比较好的改进

比如第10个常数和常字符串可以累加定义，在变量比较少时很容易不累加，但在变量比较多时，一个不留神就用了前面定义过的常数或常字符串了。这在解大方程组或复杂问题时非常实用。

• 8.对于保留结果的关键字也添加了一些

之前也有一些控制计算的关键字，但并不全面，这次集中增加了控制输出结果的关键字，有了这些关键字，再也不用在界面中设置了，还是代码省事，写一次到处粘贴就行了。

当然还有其它一些命令：

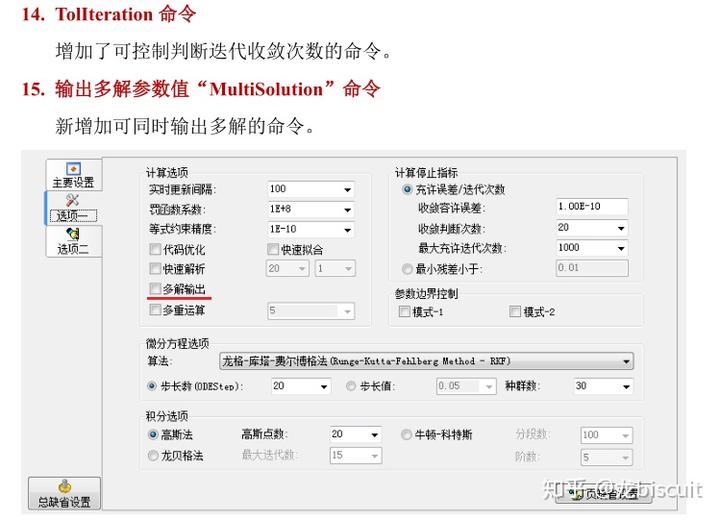
不知道MultiSolution是不是应对的多解问题。比如有些问题，帕累托解不止一个，有了这个命令，可能就能输出多个最优解了。

• 9. 编程模式代码支持fortran语言

现在使用fortran作科学计算的还不少，对fortran也比较熟悉。但在1stOpt9.0中使用fortran需要另外安装GFortran编译器就不太方便了。比如abaqus和ivf（intel 的fortran编译器）是有版本匹配的，安装GFortran时会更新掉ivf的一些东西，导致ABAQUS无法使用ivf二次开发本构模型。所以这个使用略显复杂，还是Basic和Pacsl简单实用些。当然，如果1stopt以后像自带Basic一样自带fortran编译器了，fortran应该是我的首选。

另外，8.0就已经支持python了，但感觉例子少，支持的也不好（软件老卡死），不知道是否有改进。

2021年3月16日：拿到9.0版之后发现，这个GFortran很小，安装和使用也很方便，不用自己找网上的安装，七维高科会提供。安装后并不影响其他软件，很棒！

• 10. 增加了编程模式下的调试功能

这个在使用编程模式比如basic或fortran时应该超级实用。“人非圣贤，孰能无过”呢，写错了代码要是能debug调试，那就不怕了。

之前由fortran转matlab，有很大原因是感觉每个变量都可以在工作空间清晰明了的看到其值，要是1stOpt的debug模式时能看到各变量实时的值，那就太方便了。

快捷代码模式不能debug也很正常，因为就不是一句一句运行的。所以，现在这种错误了提示行数的提醒方式也还行。

11.可以include了

之前就想，python能不能导入外部的包，没想到是编程模式可以include了。这个功能猜测应该是函数写在代码本太多，所以可以单独写到一个文档中，然后在编程模式下 “包含”进来，其实完成的是 复制代码到此处 的功能。

• 12.算法的更新及其他bug修复

---

总结：

1.此次更新，添加了很多实用的功能，还是很值得期待的！

2.我比较喜欢 向dll中传数组和循环常数数据的功能（以前只能传参数）、多页面多结果保存功能、常数及常字符串可以累加定义的功能、debug功能 以及关键字控制计算和输出功能。 当然，优化方法的改进才是最见功力的地方，只是在使用时这几个改进时应该感受最明显。

3.期望：

3.1 在人工智能、大数据的比较火的现在，希望1stOpt这方面也能独树一帜。最起码目前的表格使用方式就很方便，但表格容纳数据量不大，希望扩充表格容纳数据的能力。

3.2 说明书或提示能写详细点。有不少软件中，鼠标移动到相应按钮处就有提示，或选中代码中某关键字处，按f1键就能打开帮助文档。其实1stOpt有很多功能很棒，只是没有详细介绍导致大家并不太会用。比如什么算法什么时候用（UGO算法中寻优模式好几种，每种适用于什么），有些不常见的函数（比如SMin3：SMin3(a,b,x)的结果不是a就是b，关键在于abs(a-x)与abs(b-x)的大小，若abs(a-x)<abs(b-x),则结果为a，若abs(a-x)>abs(b-x),则结果为b。琢磨了好大会儿才明白）也没有交代什么功能。

3.3 以前flac3d3.0版本就只有4M大小（2002年），但在岩土圈也是威名赫赫，现在flac3d7.0也有上G大小了，和其余软件的数据格式交互、自身的图形界面交互、以及多核运行效率都提高了很多。希望1stOpt也能在自己的路上早日壮大。

3.4 其他小建议(在使用中随时间更新):

3.4.1 计算完有个声音提示就好了。2021年3月16日

3.4.2 默认计算结果页面没有添加图例，默认不是点线图。不知道这些在ini配置文档中能不能设定。2021年3月16日

3.4.3 不知道能不能加上多目标优化，现在1stOpt都是单目标优化。2021年3月16日

3.4.4 1stopt计算时长统计在跨过24:00时就错了。2021年5月1日

3.4.5 仅在1stOpt数据电子表格有简单的线性插值，没有matlab中interp1或复杂的插值函数。也没有光滑数据的函数。2021年5月1日

---

2022年12月7日21:28:23 做了视频，详细琢磨了一下9.0的新功能，与大家分享：

1stOpt 9.0 新特性详细介绍https://www.zhihu.com/video/1583935900261773312

具体代码：

NewCodeBlock"1stOpt 9.0 New";nnNewCodeBlock"1 多层自回归网络工具箱功能提升";nnNewCodeBlock"2 增加了线性、多项式及完全多现实拟合计算功能";nNewCodeBlock"2.1 线性拟合";nVariable x1,x2,y;nFunction y=LineFit(x1,x2);nData;nx1=[23.73,24.31,25.16,26.34,28.05,30.47,33.94,39.27,42.4,47.15,51.35,54.1,55.22];nx2=[-3.329,-4.159,-5.153,-6.63,-8.462,-10.59,-12.83,-14.84,-15.31,-15.09,-13.46,-10.82,-7.7];ny=[21.23,14.36,9.766,6.643,4.542,3.09,2.105,1.434,0.9766,0.6643,0.4542,0.309,0.2105];nNewCodeBlock"2.2 多项式拟合";nVariable x1,x2,y;nFunction y=PolyFit(x1,x2,2);nData;nx1=[23.73,24.31,25.16,26.34,28.05,30.47,33.94,39.27,42.4,47.15,51.35,54.1,55.22];nx2=[-3.329,-4.159,-5.153,-6.63,-8.462,-10.59,-12.83,-14.84,-15.31,-15.09,-13.46,-10.82,-7.7];ny=[21.23,14.36,9.766,6.643,4.542,3.09,2.105,1.434,0.9766,0.6643,0.4542,0.309,0.2105];n NewCodeBlock"2.3 完全多项式拟合";nVariable x1,x2,y;nFunction y=PolyFit2(x1,x2，2);nData;nx1=[23.73,24.31,25.16,26.34,28.05,30.47,33.94,39.27,42.4,47.15,51.35,54.1,55.22];nx2=[-3.329,-4.159,-5.153,-6.63,-8.462,-10.59,-12.83,-14.84,-15.31,-15.09,-13.46,-10.82,-7.7];ny=[21.23,14.36,9.766,6.643,4.542,3.09,2.105,1.434,0.9766,0.6643,0.4542,0.309,0.2105];nnNewCodeBlock"3 参数赋予初值为 0 时效率大幅提高";n Constant k=1.38*10^(-23);nParameter ea=0;nVariable f,tm;nFunction f=f0*exp(-Ea/(k*(Tm-Tf)));nData;nf Tm (K)n0.1 251.52n0.5 257.31n1 260.93n5 266.99n10 270.07nnNewCodeBlock"4 误差（目标）函数种类的选择";nWeightedReg = 3;nVariable T,y1,y2;nODEFunctionny1' = k0;ny2' = k1*y1*y2;nData;nT = [0 2 4 6 8 10 12];ny1=[307.18 394.39 441.93 516.62 565.13 636.74 653.68];ny2 = [21.06666667 15.4 9.633333333 4.666666667 0.753333333 0.403333333 0.206666667];nnNewCodeBlock"5 输出结果多页面保存，多页面预测";nnNewCodeBlock"6 调用外部高级语言编写的 dll 目标函数时支持循环常数（LoopConstan）传递，同时也支持数据直接从代码本传入目标函数动态库";nNewCodeBlock"6.1 快捷代码";nConstant n=10;nLoopConstant a=[1,2,3], b=[0.3,0.2,0.1];nFullLoopModel;nParameter x(0:n-1)=[-5,10];nMinFunction Sum(i=0:n-2)(a*100.0*(x[i]^2.0-x[i+1])^2.0+b*(x[i]+sin(x[i+1])-1.0)^2.0);nNewCodeBlock"6.2 调用外部高级语言编写的 dll 目标函数时支持循环常数（LoopConstan）传递"nConstant n=10;nLoopConstant a=[1,2,3], b=[0.3,0.2,0.1];nFullLoopModel;nRunDLLModel = 1;nParameter x(0:n-1)=[-5,10];nMinFunction "G:Program Files (x86)1stOpt 9.0WorkPath1stOpt 9.0 Newtest2.dll";nnNewCodeBlock"7 支持连续定义约束: SubjectTo x1>x2>x3>x4;";nNewCodeBlock"7.1 方程约束";nParameterDomain = [0,90];nFunctionncosd(5*a)+cosd(5*b)+cosd(5*c)+cosd(5*d)+cosd(5*e)+cosd(5*f)=0;ncosd(7*a)+cosd(7*b)+cosd(7*c)+cosd(7*d)+cosd(7*e)+cosd(7*f)=0;ncosd(11*a)+cosd(11*b)+cosd(11*c)+cosd(11*d)+cosd(11*e)+cosd(11*f)=0;ncosd(13*a)+cosd(13*b)+cosd(13*c)+cosd(13*d)+cosd(13*e)+cosd(13*f)=0;ncosd(17*a)+cosd(17*b)+cosd(17*c)+cosd(17*d)+cosd(17*e)+cosd(17*f)=0;ncosd(19*a)+cosd(19*b)+cosd(19*c)+cosd(19*d)+cosd(19*e)+cosd(19*f)=0;n0 <a < b < c < d < e < f < 90;nNewCodeBlock"7.2 条件约束";nParameterDomain = [0,90];nSubjectTo 0 <a < b < c < d < e < f < 90;nFunctionncosd(5*a)+cosd(5*b)+cosd(5*c)+cosd(5*d)+cosd(5*e)+cosd(5*f)=0;ncosd(7*a)+cosd(7*b)+cosd(7*c)+cosd(7*d)+cosd(7*e)+cosd(7*f)=0;ncosd(11*a)+cosd(11*b)+cosd(11*c)+cosd(11*d)+cosd(11*e)+cosd(11*f)=0;ncosd(13*a)+cosd(13*b)+cosd(13*c)+cosd(13*d)+cosd(13*e)+cosd(13*f)=0;ncosd(17*a)+cosd(17*b)+cosd(17*c)+cosd(17*d)+cosd(17*e)+cosd(17*f)=0;ncosd(19*a)+cosd(19*b)+cosd(19*c)+cosd(19*d)+cosd(19*e)+cosd(19*f)=0;nNewCodeBlock"7.3 循环形式写方程";nParameterDomain = [0,90];nConstant v=[5,7,11,13,17,19];nFunction For(i=1:6,v)(cosd(v*a)+cosd(v*b)+cosd(v*c)+cosd(v*d)+cosd(v*e)+cosd(v*f)=0);n0 < a < b < c < d < e < f < 90;nNewCodeBlock"7.4 循环形式写方程和约束";nParameterDomain = [0,90];nConstant v=[5,7,11,13,17,19];nFunction For(i=1:6,v)(Sum(i=1:6,p)(cosd(v*p))=0);nFor(i=0:6)(if(i=0,0<p[1],if(i=6, p[i]<90, p[i]<p[i+1])));nnNewCodeBlock"8 重复定义参数，服从后者";nParameter p1=[,1],p1=[0,], p2=[1,2];nMaxFunction p1+p2;nnNewCodeBlock"9 连续定义参数";nParameter -0.5<A3<0, 0<t1<t2<10, -0.5<A1<A2<0;nMaxFunction a1+a2+a3+t1+t2;nnNewCodeBlock"10 常数及常字符串可以累加定义";nNewCodeBlock"10.1 9.0之前";nConstant b=3, a=1+b+3;//每个变量只能定义一次nConstStr f=2*d +3nnNewCodeBlock"10.2 9.0版本及之后版本";nConstant a=1, b=3, a=a+b+3;//每个变量都可以定义多次nConstStr f=2*d, f=f+3;nnNewCodeBlock"11 增加迭代计算自动保存命令";nTitle "NLReg Demo - 1";nnObjAppendIteration=1;//每隔1代保存一次目标函数nObjAppendSave ="1.1 objWithIter.csv";//在当前目录下保存目标函数随迭代代数变化过程nnParAppendIteration=1;//每隔1代保存一次参数nParAppendSave="1.2 paraWithIter.csv";//在当前目录下保存参数随迭代代数变化过程nnSaveResultFile="2.1 BestResult.csv";//保存最终计算结果nSaveParameterFile="2.2 BestPara.csv"//保存最终计算最佳参数值nnParameter b1, b2, b3, b4;nVariable x, y;nFunction y=exp(b1*x)+exp(b2*x)+b3*sin(b4*x);nData;n//xtyn2t4n2.1t4.1n2.2t4.3n2.3t4.5n2.4t4.6n2.5t4.8n2.6t5.0n2.7t5.1n2.8t5.3n2.9t5.5nnNewCodeBlock"12 直接支持 Fortran 语言";nNewCodeBlock"12.1 快捷模式代码";nConstant n =5;nParameter x(n);nMinFunction Sum(i=1:n-1)(x[i]^2+x[i+1]*sin(10*pi*x[i]*x[i+1])+2+(x[i]+x[i+1])^2);nNewCodeBlock"12.2 编程模式（Basic）代码";nConstant n=5;nParameter x(n);nStartProgram [Basic];nSub MainModelndim i as integerndim td1 as doublentd1 = 0nfor i = 1 to n - 1ntd1 = td1 + x(i)^2+x(i+1)*sin(10*pi*x(i)*x(i+1))+2+(x(i)+x(i+1))^2nnextnObjectiveResult = td1nEnd SubnEndProgram;nNewCodeBlock"12.3 编程模式（Fortran）代码";nConstant n=5;nParameter x(n);nConstStr pi=dacos(-1.D0);nStartProgram [Fortran];nSubroutine MainModelninteger inreal*8 td1ntd1 = 0.0ndo i = 1, n - 1n td1 = td1 + x(i)^2.0+x(i+1)*sin(10.0*pi*x(i)*x(i+1))+2.0+(x(i)+x(i+1))^2.0nend donObjectiveResult = td1nEnd SubroutinenEndProgram;nnNewCodeBlock"编程模式（Pacsl）代码";nConstant n=5;nParameter x(n);nStartProgram [Pascal];nProcedure MainModel;nvar i: integer;ntd1: double;nBeginntd1 := 0;nfor i := 1 to n - 1 dontd1 := td1 + sqr(x[i])+x[i+1]*sin(10.0*pi*x[i]*x[i+1])+2.0+sqr(x[i]+x[i+1]);nObjectiveResult := td1;nEnd;nEndProgram;nnNewCodeBlock"13 支持 Matlab 数据文件（.mat）输入及导出";n//在 1stOpt 内置电子表格里可以打开和保存 Matlab 数据文件（.mat）nnNewCodeBlock"14 TolIteration 命令";nTitle "NLReg Demo - 1";nnObjAppendIteration=1;//每隔1代保存一次目标函数nObjAppendSave ="1.1 objWithIter.csv";//在当前目录下保存目标函数随迭代代数变化过程nnParAppendIteration=1;//每隔1代保存一次参数nParAppendSave="1.2 paraWithIter.csv";//在当前目录下保存参数随迭代代数变化过程nnSaveResultFile="2.1 BestResult.csv";//保存最终计算结果nSaveParameterFile="2.2 BestPara.csv";//保存最终计算最佳参数值nnTolIteration=100;//控制判断迭代收敛次数nnParameter b1, b2, b3, b4;nVariable x, y;nFunction y=exp(b1*x)+exp(b2*x)+b3*sin(b4*x);nData;n//xtyn2t4n2.1t4.1n2.2t4.3n2.3t4.5n2.4t4.6n2.5t4.8n2.6t5.0n2.7t5.1n2.8t5.3n2.9t5.5nnNewCodeBlock"15 输出多解参数值“MultiSolution”命令";nTitle "NLReg Demo - 1";nnObjAppendIteration=1;//每隔1代保存一次目标函数nObjAppendSave ="1.1 objWithIter.csv";//在当前目录下保存目标函数随迭代代数变化过程nnParAppendIteration=1;//每隔1代保存一次参数nParAppendSave="1.2 paraWithIter.csv";//在当前目录下保存参数随迭代代数变化过程nnSaveResultFile="2.1 BestResult.csv";//保存最终计算结果nSaveParameterFile="2.2 BestPara.csv";//保存最终计算最佳参数值nnTolIteration=100;//控制判断迭代收敛次数nnMultiSolution=true;//同时输出多解nnParameter b1, b2, b3, b4;nVariable x, y;nFunction y=exp(b1*x)+exp(b2*x)+b3*sin(b4*x);nData;n//xtyn2t4n2.1t4.1n2.2t4.3n2.3t4.5n2.4t4.6n2.5t4.8n2.6t5.0n2.7t5.1n2.8t5.3n2.9t5.5nnNewCodeBlock"16 编程模式下新增“DebugModel”命令";nNewCodeBlock"16.1 Basic !!!卡死";nDebugModel=ture;nConstant n=5;nParameter x(n);nStartProgram [Basic];nSub MainModelndim i as integerndim td1 as doublentd1 = 0nfor i = 1 to n - 1ntd1 = td1 + x(i)^2+x(i+1)*sin(10*pi*x(i)*x(i+1))+2+(x(i)+x(i+1))^2nnextnObjectiveResult = td1nEnd SubnEndProgram;nNewCodeBlock"16.2 Fortran";n//DebugModel=ture;//能给出错误原因，如果代码正确给出编译成功的的提示，并不会开始计算nConstant n=5;nParameter x(n);nConstStr pi=dacos(-1.D0);nStartProgram [Fortran];nSubroutine MainModelninteger inreal*8 td1ntd1 = 0.0ndo i = 1, n - 1n td1 = td1 + x(i)^2.0+x(i+1)*sin(10.0*pi*x(i)*x(i+1))+2.0+(x(i)+x(i+1))^2.0nend donObjectiveResult = td1nEnd SubroutinenEndProgram;nNewCodeBlock"17 “IncludeFile”，编程模式下增加外部代码单元，编程模式下可通该命令调用相关代码单元。";nNewCodeBlock "17.1 NNFit in Fortran Model (2-3-1) 无IncludeFile";n//DebugModel=ture;//能给出错误原因，如果代码正确给出编译成功的的提示，并不会开始计算n//NNFit(NS=[2-3-1], TF=[1,1], DN=[1,1], NC=1, CT=2, Code=3);nAlgorithm = UGO1[30];nConstantn RMin = -1.0, RMax = 1.0, //输入数据归一化上下限值n SMin = 0.1, SMax = 0.9, //输出数据归一化上下限值n Minx1 = 0.0, Maxx1 = 1.0, //最小最大值 (变量 x1)n Minx2 = 0.0, Maxx2 = 1.0, //最小最大值 (变量 x2)n Miny = 0.0, Maxy = 1.0; //最小最大值 (变量 y)nParameter p(13);nVariable x1, x2, y[OutPut];nStartProgram [Fortran];n Function TFH(v) !Sigmoid (隐含层转换函数)n real*8 vn TFH = 1/(1+exp(-v))n end functionnn Function TFO(v) !Sigmoid (输出层转换函数)n real*8 vn TFO = 1/(1+exp(-v))n end functionnnSubroutine MainModeln integer in real*8 xx1, xx2, s11, h11, s12, h12, s13, h13, s21, h21nn do i = 0, DataLength - 1n xx1 = RMin+(RMax-RMin)*(x1(i)-Minx1)/(Maxx1-Minx1) !输入数据归一化至 [-1,1]n xx2 = RMin+(RMax-RMin)*(x2(i)-Minx2)/(Maxx2-Minx2) !输入数据归一化至 [-1,1]n s11 = p1*xx1+p4*xx2+p10 !输入至节点-1 (隐含层-1)n h11 = TFH(s11) !节点输出 (节点-1, 隐含层-1)n s12 = p2*xx1+p5*xx2+p11 !输入至节点-2 (隐含层-1)n h12 = TFH(s12) !节点输出 (节点-2, 隐含层-1)n s13 = p3*xx1+p6*xx2+p12 !输入至节点-3 (隐含层-1)n h13 = TFH(s13) !节点输出 (节点-3, 隐含层-1)n s21 = p7*h11+p8*h12+p9*h13+p13 !输入至节点-1 (输出层)n h21 = TFO(s21) !节点输出 (节点-1, 输出层)nn y(i) = Miny+(h21-SMin)*(Maxy-Miny)/(SMax-SMin) !输出数据还原yn end donnEnd SubroutinenEndProgram;nData; //训练数据nx1 = [1,1,0,0];nx2 = [1,0,1,0];ny = [1,0,0,0];nnNewCodeBlock "17.2 NNFit in Fortran Model (2-3-1) IncludeFile";n//DebugModel=ture;//能给出错误原因，如果代码正确给出编译成功的的提示，并不会开始计算n//NNFit(NS=[2-3-1], TF=[1,1], DN=[1,1], NC=1, CT=2, Code=3);nIncludeFile="G:Program Files (x86)1stOpt 9.0WorkPath1stOpt 9.0 NewsubFunc.f90";nAlgorithm = UGO1[30];nConstantn RMin = -1.0, RMax = 1.0, //输入数据归一化上下限值n SMin = 0.1, SMax = 0.9, //输出数据归一化上下限值n Minx1 = 0.0, Maxx1 = 1.0, //最小最大值 (变量 x1)n Minx2 = 0.0, Maxx2 = 1.0, //最小最大值 (变量 x2)n Miny = 0.0, Maxy = 1.0; //最小最大值 (变量 y)nParameter p(13);nVariable x1, x2, y[OutPut];nStartProgram [Fortran];n// Function TFH(v) !Sigmoid (隐含层转换函数)n// real*8 vn// TFH = 1/(1+exp(-v))n// end functionnn// Function TFO(v) !Sigmoid (输出层转换函数)n// real*8 vn// TFO = 1/(1+exp(-v))n// end functionnnSubroutine MainModeln integer in real*8 xx1, xx2, s11, h11, s12, h12, s13, h13, s21, h21nn do i = 0, DataLength - 1n xx1 = RMin+(RMax-RMin)*(x1(i)-Minx1)/(Maxx1-Minx1) !输入数据归一化至 [-1,1]n xx2 = RMin+(RMax-RMin)*(x2(i)-Minx2)/(Maxx2-Minx2) !输入数据归一化至 [-1,1]n s11 = p1*xx1+p4*xx2+p10 !输入至节点-1 (隐含层-1)n h11 = TFH(s11) !节点输出 (节点-1, 隐含层-1)n s12 = p2*xx1+p5*xx2+p11 !输入至节点-2 (隐含层-1)n h12 = TFH(s12) !节点输出 (节点-2, 隐含层-1)n s13 = p3*xx1+p6*xx2+p12 !输入至节点-3 (隐含层-1)n h13 = TFH(s13) !节点输出 (节点-3, 隐含层-1)n s21 = p7*h11+p8*h12+p9*h13+p13 !输入至节点-1 (输出层)n h21 = TFO(s21) !节点输出 (节点-1, 输出层)nn y(i) = Miny+(h21-SMin)*(Maxy-Miny)/(SMax-SMin) !输出数据还原yn end donnEnd SubroutinenEndProgram;nData; //训练数据nx1 = [1,1,0,0];nx2 = [1,0,1,0];ny = [1,0,0,0];nnNewCodeBlock"18 图形指标格式设定";nConstant Z=0.934,lamda=0.135,kappa=0.04,ps=2199;n//XAxis = Ln(p);可将横坐标设置为对数坐标。n//YAxis = Ln(OutPut);可将纵坐标设置为对数坐标。nParameter chi;nVariable p,e;nFunction e=Z-lamda*ln((p+ps)/(1+ps))-(lamda-kappa)*ln(((2/(1-chi))*p+ps)/(p+ps)) ;ndata;//p en33.7641083 0.9264706n50.0249879 0.9215686n76.9447268 0.9225490n86.0913166 0.9176471n94.5387283 0.9156863n109.8121530 0.9127451n132.4192792 0.9117647n159.6805547 0.9137255n178.6621354 0.9029412n188.9830110 0.9107843n203.6775158 0.8980392n236.5831118 0.9029412n245.6087882 0.8980392n290.6796537 0.8892157n357.1457846 0.8921569n363.8945990 0.8852941n447.1018883 0.8794118n447.1018883 0.8725490n603.2367686 0.8705882n603.2367686 0.8588235n674.9448574 0.8627451n727.4256619 0.8568627n844.9466108 0.8578431n893.7571151 0.8441176n1038.1501298 0.8450980n1038.1501298 0.8313725n1183.5067295 0.8352941n1228.6576649 0.8294118n1349.2154348 0.8235294n1374.7109188 0.8186275n1538.1258460 0.8147059n1596.8055467 0.8078431n1889.8301103 0.7911765n2195.1460202 0.7705882n2321.9542503 0.7676471n2321.9542503 0.7588235n2697.0829833 0.7490196n2697.0829833 0.7362745n3074.7150813 0.7294118n3132.8165135 0.7235294nnNewCodeBlock"字符串公式 6.0版本新增";nConstStrnf(v,w)=v+w;nConstant v=1,w=40;nf(v,w) //

下面是存在百度网盘中的附件：

链接：https://pan.baidu.com/s/1tEwPF3yT-t5z3jLdYlhxTQ?pwd=whg6

提取码：whg6

---

当前时间：2022年12月14日22:17:28

1stOpt 10.0 新特性：

1stOpt 10.0新特性https://www.zhihu.com/video/1586484876475265025

NewCodeBlock"1stOpt 10.0 主要新增功能";nnNewCodeBlock"1 神经网络拟合工具箱及相关命令";nNewCodeBlock "1.1 5-bit parity - NNFit in Quick Model (5-3-1)";nFunction NNFit(NS=[5-3-1], TF=[1,4], DN=[1,1], NC=2, CT=1, Code=1, Importance);n//Neural Network ： NNFitn// network structure： NS=[5-3-1]:3层，每层分别有5/3/1个结点，第一层是输入层（自变量），最后一层为输出层（因变量），中间是隐藏层n// Transfer function ：TF=[1,4] ,1代表隐藏层为第1种激活函数即Sigmoid 函数，4代表输出层神经元采用的第4种激活函数即Linear函数。TF长度随隐藏层层数变化n// Data normalization ：DN=[1,1]，1表示归一化，0表示不归一化。第1个1表示输入层归一化，第2个1表示输出层归一化。n// Network Connection Type： NC=2，1表示多层向前，2表示多层全向前n// code type：CT=1 ，1表示Quick Model，2表示Fortran，3表示Pascal，4表示Basic，5表示Pythonn// 代码形式：Code=1 ，1表示精简，2代表精简（表达式），3代表完全n//Importance 代表进行 输入变量重要性分析nData; //训练数据nx1 = [0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1];nx2 = [0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1];nx3 = [0,0,0,0,1,1,1,1,0,0,0,0,1,1,1,1,0,0,0,0,1,1,1,1,0,0,0,0,1,1,1,1];nx4 = [0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1];nx5 = [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1];ny = [0,1,1,0,1,0,0,1,1,0,0,1,0,1,1,0,1,0,0,1,0,1,1,0,0,1,1,0,1,0,0,1];nnNewCodeBlock "1.2 iris - NNFit in Pascal Model (4-2-1)";nDataFileWeight = [1,0];nFunction NNFit(NS=[4-2-1], TF=[1,1], DN=[1,1], NC=1, CT=3, Code=1);nData; //训练数据nx1 = [4.7,4.6,5.0,5.4,4.6,4.4,5.4,4.8,4.3,5.8,5.7,5.4,5.1,5.1,5.4,5.1,4.8,5.0,5.2,5.2,4.7,4.8,5.2,5.5,5.1,4.5,4.4,5.0,5.1,4.8,5.1,4.6,5.3,5.0,6.4,6.9,6.5,5.7,6.3,6.6,5.2,5.0,5.9,6.0,6.1,5.6,5.8,6.2,5.9,6.1,6.3,6.1,6.6,6.8,6.7,6.0,5.7,5.5,5.5,5.8,6.0,5.6,5.5,5.5,6.1,5.8,5.6,5.7,5.1,5.7,6.3,5.8,7.1,6.3,7.6,4.9,7.3,6.7,6.5,6.4,6.8,5.8,6.5,7.7,7.7,6.9,5.6,6.3,6.1,7.2,7.4,7.9,6.3,7.7,6.4,6.0,6.9,6.7,5.8,6.8,6.7,6.7,6.3,6.5,6.2];nx2 = [3.2,3.1,3.6,3.9,3.4,2.9,3.7,3.0,3.0,4.0,4.4,3.9,3.5,3.8,3.4,3.7,3.4,3.4,3.5,3.4,3.2,3.1,4.1,3.5,3.4,2.3,3.2,3.5,3.8,3.0,3.8,3.2,3.7,3.3,3.2,3.1,2.8,2.8,3.3,2.9,2.7,2.0,3.0,2.2,2.9,3.0,2.7,2.2,3.2,2.8,2.5,2.8,3.0,2.8,3.0,2.9,2.6,2.4,2.4,2.7,3.4,3.0,2.5,2.6,3.0,2.6,2.7,2.9,2.5,2.8,3.3,2.7,3.0,2.9,3.0,2.5,2.9,2.5,3.2,2.7,3.0,2.8,3.0,3.8,2.6,3.2,2.8,2.7,3.0,3.0,2.8,3.8,2.8,3.0,3.1,3.0,3.1,3.1,2.7,3.2,3.3,3.0,2.5,3.0,3.4];nx3 = [1.3,1.5,1.4,1.7,1.4,1.4,1.5,1.4,1.1,1.2,1.5,1.3,1.4,1.5,1.7,1.5,1.9,1.6,1.5,1.4,1.6,1.6,1.5,1.3,1.5,1.3,1.3,1.6,1.9,1.4,1.6,1.4,1.5,1.4,4.5,4.9,4.6,4.5,4.7,4.6,3.9,3.5,4.2,4.0,4.7,4.5,4.1,4.5,4.8,4.0,4.9,4.7,4.4,4.8,5.0,4.5,3.5,3.8,3.7,3.9,4.5,4.1,4.0,4.4,4.6,4.0,4.2,4.2,3.0,4.1,6.0,5.1,5.9,5.6,6.6,4.5,6.3,5.8,5.1,5.3,5.5,5.1,5.5,6.7,6.9,5.7,4.9,4.9,4.9,5.8,6.1,6.4,5.1,6.1,5.5,4.8,5.4,5.6,5.1,5.9,5.7,5.2,5.0,5.2,5.4];nx4 = [0.2,0.2,0.2,0.4,0.3,0.2,0.2,0.1,0.1,0.2,0.4,0.4,0.3,0.3,0.2,0.4,0.2,0.4,0.2,0.2,0.2,0.2,0.1,0.2,0.2,0.3,0.2,0.6,0.4,0.3,0.2,0.2,0.2,0.2,1.5,1.5,1.5,1.3,1.6,1.3,1.4,1.0,1.5,1.0,1.4,1.5,1.0,1.5,1.8,1.3,1.5,1.2,1.4,1.4,1.7,1.5,1.0,1.1,1.0,1.2,1.6,1.3,1.3,1.2,1.4,1.2,1.3,1.3,1.1,1.3,2.5,1.9,2.1,1.8,2.1,1.7,1.8,1.8,2.0,1.9,2.1,2.4,1.8,2.2,2.3,2.3,2.0,1.8,1.8,1.6,1.9,2.0,1.5,2.3,1.8,1.8,2.1,2.4,1.9,2.3,2.5,2.3,1.9,2.0,2.3];ny = [1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3];nData; //验证数据；预测正确，但绘图不正确nx1 = [4.7,4.6,5.0,5.4,4.6,4.4,5.4,4.8,4.3];nx2 = [3.2,3.1,3.6,3.9,3.4,2.9,3.7,3.0,3.0];nx3 = [1.3,1.5,1.4,1.7,1.4,1.4,1.5,1.4,1.1];nx4 = [0.2,0.2,0.2,0.4,0.3,0.2,0.2,0.1,0.1];ny = [1,1,1,1,1,1,1,1,1];nnNewCodeBlock "xor - NNFit in Quick Model (2-1-1)";nFunction NNFit(NS=[2-1-1], TF=[1,4], DN=[0,0], NC=2, CT=1, Code=1);nData; //训练数据nx1 = [0,0,1,1];nx2 = [0,1,0,1];ny = [0,1,1,0];nnNewCodeBlock "xor - NNFit in Quick Model (2-1-1)";nSharedModel;nFunction NNFit(NS=[2-1-1], TF=[1,4], DN=[0,0], NC=2, CT=1, Code=1);nData; //训练数据nx1 = [0,0,1];nx2 = [0,1,0];ny = [0,1,1];nData; //训练数据nx1 = [1];nx2 = [1];ny = [0];nnNewCodeBlock "xor - NNFit in Quick Model (2-1-1)";nSharedModel;nDataFileWeight = [1,0];nFunction NNFit(NS=[2-1-1], TF=[1,4], DN=[0,0], NC=2, CT=1, Code=1);nData; //训练数据nx1 = [0,0,1,1];nx2 = [0,1,0,1];ny = [0,1,1,0];nData; //验证数据nx1 = [1];nx2 = [1];ny = [0];nnNewCodeBlock "xor - NNFit in Fortran Model (2-1-1)";n//NNFit(NS=[2-1-1], TF=[1,4], DN=[0,0], NC=2, CT=2, Code=3);nAlgorithm = UGO1[30];nParameter p(7);nDataFileWeight = [1,0];nVariable x1, x2, y[OutPut];nStartProgram [Fortran];n Function TFH(v) !Sigmoid (隐含层转换函数)n real*8 vn TFH = 1/(1+exp(-v))n end functionnn Function TFO(v) !Linear (输出层转换函数)n real*8 vn TFO = vn end functionnnSubroutine MainModeln integer in real*8 xx1, xx2, s11, h11, s21, h21nn do i = 0, DataLength - 1n xx1 = x1(i) !输入数据非归一化n xx2 = x2(i) !输入数据非归一化n s11 = p1*xx1+p2*xx2+p6 !输入至节点-1 (隐含层-1)n h11 = TFH(s11) !节点输出 (节点-1, 隐含层-1)n s21 = p3*h11+p7+p4*xx1+p5*xx2 !输入至节点-1 (输出层)n h21 = TFO(s21) !节点输出 (节点-1, 输出层)nn y(i) = h21n end donnEnd SubroutinenEndProgram;nData; //训练数据nx1 = [0,0,1,1];nx2 = [0,1,0,1];ny = [0,1,1,0];nData; //验证数据nx1 = [1];nx2 = [1];ny = [0];nnNewCodeBlock "xor - NNFit in Fortran Model (2-1-1)";n//NNFit(NS=[2-1-1], TF=[1,4], DN=[0,0], NC=2, CT=2, Code=2);nAlgorithm = UGO1[30];nParameter p(7);nDataFileWeight = [1,0];nVariable x1, x2, y[OutPut];nStartProgram [Fortran];nSubroutine MainModeln integer in do i = 0, DataLength - 1n y(i) = p3*(1/(1+exp(-(p1*x1(i)+p2*x2(i)+p6))))+p7+p4*x1(i)+p5*x2(i)n end donEnd SubroutinenEndProgram;nData; //训练数据nx1 = [0,0,1,1];nx2 = [0,1,0,1];ny = [0,1,1,0];nData; //验证数据nx1 = [1];nx2 = [1];ny = [0];nnNewCodeBlock "xor - NNFit in Fortran Model (2-1-1)";nDataFileWeight = [1,0];nFunction NNFit(NS=[2-1-1], TF=[1,4], DN=[0,0], NC=2, CT=2, Code=1);nData; //训练数据nx1 = [0,0,1,1];nx2 = [0,1,0,1];ny = [0,1,1,0];nData; //验证数据nx1 = [1];nx2 = [1];ny = [0];nnNewCodeBlock "xor - NNFit in Quick Model (2-1-1)";nSharedModel;nDataFileWeight = [1,0];nFunction NNFit(NS=[2-1-1], TF=[1,4], DN=[0,0], NC=2, CT=1, Code=1);nData; //训练数据nx1 = [0,0,1,1];nx2 = [0,1,0,1];ny = [0,1,1,0];nData; //验证数据nx1 = [1];nx2 = [1];ny = [0];nnNewCodeBlock "xor - NNFit in Quick Model (2-1-1)";n//NNFit(NS=[2-1-1], TF=[1,4], DN=[0,0], NC=2, CT=1, Code=3);nAlgorithm = UGO1[30];nConstStrn TFH(v) = 1/(1+exp(-v)), //Sigmoid (隐含层转换函数)n TFO(v) = v, //Linear (输出层转换函数)n xx1 = x1, //输入数据非归一化n xx2 = x2, //输入数据非归一化n s11 = p1*xx1+p2*xx2+p6, //输入至节点-1 (隐含层-1)n h11 = TFH(s11), //节点输出 (节点-1, 隐含层-1)n s21 = p3*h11+p7+p4*xx1+p5*xx2, //输入至节点-1 (输出层)n h21 = TFO(s21); //节点输出 (节点-1, 输出层)nParameter p(7);nDataFileWeight = [1,0];nSharedModel;nVariable x1, x2, y;nFunction y = h21;nData; //训练数据nx1 = [0,0,1,1];nx2 = [0,1,0,1];ny = [0,1,1,0];nData; //验证数据nx1 = [1];nx2 = [1];ny = [0];nnnnNewCodeBlock"2 拟合计算可输出参数标准差及置信度";n//There are many test examples located in the folder: examplesnn//Nonlinear regression: any No. of variables and parameters, any user-defined functionnTitle "NLReg Demo - 1";nConfidenceLevel = 0.95;nParameter b1, b2, b3, b4;nVariable x, y;nFunction y=exp(b1*x)+exp(b2*x)+b3*sin(b4*x);nData;n//xtyn2t4n2.1t4.1n2.2t4.3n2.3t4.5n2.4t4.6n2.5t4.8n2.6t5.0n2.7t5.1n2.8t5.3n2.9t5.5nNewCodeBlock"3 可定义三维、四维及五维参数（Parameter）、传递参数（PassParameter）及常数";nConstant D(7,3)=[4,4,3,n3,3,2,n3,3,2,n3,2,3,n4,3,3,n2,2,1,n3,2,2]; //二维数组nBinParameter x(12,7,3);//工人 i 被安排到第 j 天第 k 个班次，三维数组！nAlgorithm = LP;nPassParameter w=Sum(i=1:12)(Sum(j=1:7)(x[i,j,1]));nMinFunction Sum(i=1:12)(Sum(j=1:7)(x[i,j,1]));nFor(i=1:12)(For(j=1:7)(Sum(k=1:3)(x[i,j,k])<=1));//每人每天最多工作一个班次nFor(i=1:12)(For(j=1:6)(x[i,j,3]+x[i,j+1,1]<=1)); //每人在任何时候都不能连续两个班次工作nFor(i=1:12)(x[i,7,3]+x[i,1,1]<=1);nFor(i=1:12)(Sum(j=1:7)(Sum(k=1:3)(x[i,j,k]))<=5);//每人每周至少休息两天nfor(j=1:7)(for(k=1:3)(Sum(i=1:12)(x[i,j,k])>=d[j,k]));//每个班次人数满足需求nnNewCodeBlock"4 Latex 及 MathXL 公式支持";n y=exp(b1*x)+exp(b2*x)+b3*sin(b4*x);nnNewCodeBlock"5 拟合预测可以计算曲线一阶至五阶导数值";nParameter a=[1,3],b=[2,4],c=[3,5];//要优化的参数及其范围nVariable t,y;//变量nFunction y=a*t^2+b*t+c;nData;n//t y 变量顺序要和Variable后变量对应n-5 39n-4 24n-3 13n-2 6n-1 3n0 4n1 9n2 18n3 31n4 48n5 69nnnnNewCodeBlock"6 “SharingPar”关键字";n//1）SharingPar = 0，无作用；n//2）SharingPar = 1，前一最优解作为后一的参数初值，对所有参数，无论该n//参数最初是否设定有初值；n//3）SharingPar = 2，对没有设定初值的参数，前一最优解作为后一的参数初n//值，对最初已设定了初值得参数，仍使用最初设定的参数；n//4）SharingPar = 3，前面所有计算参数最优解的平均值作为后一的参数初值，n//对所有参数，无论该参数最初是否设定有初值；n//5）SharingPar = 4，对没有设定初值的参数，前面所有组参数最优解的平均n//值作为后一组的参数初值，对最初已设定了初值得参数，仍使用最初设定的n//参数；nnNewCodeBlock"6.1 csuh g-up";n Title "绘制csuh本构模型塑性势面";n SharingPar = 1nConstant M=1.25,xm=1.8,kesi=0.0974462633886968,py=4.619;nConstStr Mc=M*exp(-xm*kesi);nLoopConstant p=[1e-10:0.01:py];nParameter q=[0,];nPlotLoopData p[x],q[y];nFunction ln(p/py)+ln(1+q^2/(Mc^2*p^2))=0;nnNewCodeBlock"6.2 csuh g-low";n Title "绘制csuh本构模型塑性势面";nSharingPar = 1nConstant M=0.883789546430,xm=1.8,kesi=0.0974462633886968,py=4.619;nConstStr Mc=M*exp(-xm*kesi);nLoopConstant p=[1e-10:0.01:py];nParameter q=[-5,0];nPlotLoopData p[x],q[y];nFunction ln(p/py)+ln(1+q^2/(Mc^2*p^2))=0;nnNewCodeBlock"7 高价微分方程简写";nNewCodeBlock"7.1 10.0版本之前的写法";nConstant e=exp(1);nVariable x=[0,1],u=[1,1/e],u''=[1,1/e],u''''=[1,1/e],u''''''=[1,1/e],u''''''''=[1,1/e],u''''''''''=[1,1/e];nPlot x[x],u,u',u'',u''';nODEFunction u’’’’’’’’’’’’=2*exp(x)*u''+u''';nNewCodeBlock"7.2 10.0版本的写法";nConstant e=exp(1);nVariable x=[0,1],u=[1,1/e],u(2')=[1,1/e],u(4')=[1,1/e],u(6')=[1,1/e],u(8')=[1,1/e],u(10')=[1,1/e];nPlot x[x],u,u',u'',u''';nODEFunction u(12')=2*exp(x)*u''+u''';nnNewCodeBlock"8 增加“SumAnd”和“SumOr”函数；";nNewCodeBlock"8.1 10.0版本之前的写法";nConstant n=15; //天数nConstant a=[25,16,24,17,29,25,22,28,21,17,28,14,12,25,11]; //人数nConstant p=[208,212,213,217,206,203,212,214,200,204,208,209,219,216,214]; //费用nIntParameter x(n);nAlgorithm = LP;nMinFunction Sum(i=1:n,x)(x*p[i]);nFor(i=1:n)(Sum(j=1:n)(if((j<>Wrap(i+1,n))and(j<>Wrap(i+2,n))and(j<>Wrap(i+3,n))and(j<>Wrap(i+4,n))and(j<>nWrap(i+5,n)),x[j]))>=a[i]);nnnNewCodeBlock"8.2 10.0版本的简化写法";nConstant n=15; //天数nConstant a=[25,16,24,17,29,25,22,28,21,17,28,14,12,25,11]; //人数nConstant p=[208,212,213,217,206,203,212,214,200,204,208,209,219,216,214]; //费用nIntParameter x(n);nAlgorithm = LP;nMinFunction Sum(i=1:n,x)(x*p[i]);nFor(i=1:n)(Sum(j=1:n)(if(SumAnd(k=1:5)(j<>Wrap(i+k,n)),x[j]))>=a[i]);nnNewCodeBlock"9. 批量定义范围：LowBound，UpBound";nNewCodeBlock"9.1 10.0版本之前的写法";nParameter x1=[-2.3,2.3], x2=[-2.3,2.3], x3=[-3.2,3.2], x4=[-3.2,3.2], x5=[-3.2,3.2];nMinFunction exp(Prod(i=1:5)(x[i]));nSum(i=1:5)(x[i]^2)-10=0;nx2*x3-5*x4*x5=0;nx1^3+x2^3+1=0;nNewCodeBlock"9.2 10.0版本的写法";nParameter x(5);nLowBound = -[2.3,2.3,3.2,3.2,3.2];nUpBound = [2.3,2.3,3.2,3.2,3.2];nMinFunction exp(Prod(i=1:5)(x[i]));//+a1+a2;nSum(i=1:5)(x[i]^2)-10=0;nx2*x3-5*x4*x5=0;nx1^3+x2^3+1=0;nnNewCodeBlock"10 “?”定义 Sheet 或 CodeSheet 范围，可自动获取数据范围";nTitle "NLReg Demo - 1";nConfidenceLevel = 0.95;nParameter b1, b2, b3, b4;nVariable x, y;nFunction y=exp(b1*x)+exp(b2*x)+b3*sin(b4*x);nDataFile "CodeSheet1[A1:B?]";nnNewCodeBlock"11 矩阵计算功能强化";n//矩阵相加：AddMat()；n//矩阵相减：SubMat()；n//矩阵相乘：MultMat()；n//矩阵求逆：InvMat()；n//矩阵转置：TransMat()；n//矩阵表达式展开：MatrixStr()；n//矩阵操作：Matrix()nNewCodeBlock"11.1 矩阵解法1";nConstant c(11,11)=[1,1,1,1,1,1,1,1,1,1,1,n1,1.1,1.1^2,1.1^3,1.1^4,1.1^5,1.1^6,1.1^7,1.1^8,1.1^9,1.1^10,n1,1.2,1.2^2,1.2^3,1.2^4,1.2^5,1.2^6,1.2^7,1.2^8,1.2^9,1.2^10,n1,1.3,1.3^2,1.3^3,1.3^4,1.3^5,1.3^6,1.3^7,1.3^8,1.3^9,1.3^10,n1,1.4,1.4^2,1.4^3,1.4^4,1.4^5,1.4^6,1.4^7,1.4^8,1.4^9,1.4^10,n1,1.5,1.5^2,1.5^3,1.5^4,1.5^5,1.5^6,1.5^7,1.5^8,1.5^9,1.5^10,n1,1.6,1.6^2,1.6^3,1.6^4,1.6^5,1.6^6,1.6^7,1.6^8,1.6^9,1.6^10,n1,1.7,1.7^2,1.7^3,1.7^4,1.7^5,1.7^6,1.7^7,1.7^8,1.7^9,1.7^10,n1,1.8,1.8^2,1.8^3,1.8^4,1.8^5,1.8^6,1.8^7,1.8^8,1.8^9,1.8^10,n1,1.9,1.9^2,1.9^3,1.9^4,1.9^5,1.9^6,1.9^7,1.9^8,1.9^9,1.9^10,n1,2.0,2.0^2,2.0^3,2.0^4,2.0^5,2.0^6,2.0^7,2.0^8,2.0^9,2.0^10];nConstant p(11,1)=[0,0,0,0,0,pi,0,0,0,0,0];nd=InvMat(c);nx=MultMat(d,p);nNewCodeBlock"11.2 矩阵解法2 最方便快捷";nConstant c(11,11)=[1,1,1,1,1,1,1,1,1,1,1,n1,1.1,1.1^2,1.1^3,1.1^4,1.1^5,1.1^6,1.1^7,1.1^8,1.1^9,1.1^10,n1,1.2,1.2^2,1.2^3,1.2^4,1.2^5,1.2^6,1.2^7,1.2^8,1.2^9,1.2^10,n1,1.3,1.3^2,1.3^3,1.3^4,1.3^5,1.3^6,1.3^7,1.3^8,1.3^9,1.3^10,n1,1.4,1.4^2,1.4^3,1.4^4,1.4^5,1.4^6,1.4^7,1.4^8,1.4^9,1.4^10,n1,1.5,1.5^2,1.5^3,1.5^4,1.5^5,1.5^6,1.5^7,1.5^8,1.5^9,1.5^10,n1,1.6,1.6^2,1.6^3,1.6^4,1.6^5,1.6^6,1.6^7,1.6^8,1.6^9,1.6^10,n1,1.7,1.7^2,1.7^3,1.7^4,1.7^5,1.7^6,1.7^7,1.7^8,1.7^9,1.7^10,n1,1.8,1.8^2,1.8^3,1.8^4,1.8^5,1.8^6,1.8^7,1.8^8,1.8^9,1.8^10,n1,1.9,1.9^2,1.9^3,1.9^4,1.9^5,1.9^6,1.9^7,1.9^8,1.9^9,1.9^10,n1,2.0,2.0^2,2.0^3,2.0^4,2.0^5,2.0^6,2.0^7,2.0^8,2.0^9,2.0^10];nConstant p(11,1)=[0,0,0,0,0,pi,0,0,0,0,0];nx=Matrix(c^Inv*p);nNewCodeBlock"11.3 优化方法求解-1";nAlgorithm = SM2;nConstant c(0:10,0:10)=[1,1,1,1,1,1,1,1,1,1,1,n1,1.1,1.1^2,1.1^3,1.1^4,1.1^5,1.1^6,1.1^7,1.1^8,1.1^9,1.1^10,n1,1.2,1.2^2,1.2^3,1.2^4,1.2^5,1.2^6,1.2^7,1.2^8,1.2^9,1.2^10,n1,1.3,1.3^2,1.3^3,1.3^4,1.3^5,1.3^6,1.3^7,1.3^8,1.3^9,1.3^10,n1,1.4,1.4^2,1.4^3,1.4^4,1.4^5,1.4^6,1.4^7,1.4^8,1.4^9,1.4^10,n1,1.5,1.5^2,1.5^3,1.5^4,1.5^5,1.5^6,1.5^7,1.5^8,1.5^9,1.5^10,n1,1.6,1.6^2,1.6^3,1.6^4,1.6^5,1.6^6,1.6^7,1.6^8,1.6^9,1.6^10,n1,1.7,1.7^2,1.7^3,1.7^4,1.7^5,1.7^6,1.7^7,1.7^8,1.7^9,1.7^10,n1,1.8,1.8^2,1.8^3,1.8^4,1.8^5,1.8^6,1.8^7,1.8^8,1.8^9,1.8^10,n1,1.9,1.9^2,1.9^3,1.9^4,1.9^5,1.9^6,1.9^7,1.9^8,1.9^9,1.9^10,n1,2.0,2.0^2,2.0^3,2.0^4,2.0^5,2.0^6,2.0^7,2.0^8,2.0^9,2.0^10];nConstant p(0:10)=[0,0,0,0,0,pi,0,0,0,0,0];nParameter x(0:10);nFunction For(i=0:10)(Sum(j=0:10)(x[j]*c[i,j])=p[i]);nnNewCodeBlock"11.4 优化方法求解-2";nAlgorithm = SM2;nFunction For(i=0:10)(Sum(j=0:10)(x[j]*(1+i*0.1)^j)=if(i=5,pi,0));nnnNewCodeBlock"12 复数拟合功能的改进和增强；";nNewCodeBlock"12.1 分解拟合代码";nVariable x,y1,y2;nSharedModel;nFunction y1 = a/(1+(b*x)^2);ny2 = -(a*c)/(1+(n*x)^2);nData;n0 3 -0.789n0.01 2.88462 -0.660n0.02 2.58621 -0.648n0.03 2.20588 -0.511n0.04 1.82927 -0.440n0.05 1.5 -0.418n0.06 1.22951 -0.338n0.07 1.01351 -0.279n0.08 0.8427 -0.237n0.09 0.70755 -0.218n0.1 0.6 -0.177n0.11 0.5137 -0.136nNewCodeBlock"12.2 直接拟合代码";nComplexStr = i;nVariable x,y[realPart],y[imagPart];nFunction y= A/(1+(x*B)^2) - i*(A*C)/(1+(x*B)^2);nData;n0 3 -0.789n0.01 2.88462 -0.660n0.02 2.58621 -0.648n0.03 2.20588 -0.511n0.04 1.82927 -0.440n0.05 1.5 -0.418n0.06 1.22951 -0.338n0.07 1.01351 -0.279n0.08 0.8427 -0.237n0.09 0.70755 -0.218n0.1 0.6 -0.177n0.11 0.5137 -0.136nnNewCodeBlock"13 “MDataSet”功能改进；";nNewCodeBlock"13.1 pascal 最短路径问题";nConstant n = 8;nParameters Cities(1:n)=[1,n,0];nConstant Dis(0:n+1,0:n+1) = [0,2,5,1,1000,1000,1000,1000,1000,1000,n2,0,1000,1000,12,14,10,1000,1000,1000,n5,1000,0,1000,6,10,4,1000,1000,1000,n1,1000,1000,0,13,12,11,1000,1000,1000,n1000,12,6,13,0,1000,1000,3,9,1000,n1000,14,10,12,1000,0,1000,6,5,1000,n1000,10,4,11,1000,1000,0,8,10,1000,n1000,1000,1000,1000,3,6,8,0,1000,5,n1000,1000,1000,1000,9,5,10,1000,0,2,n1000,1000,1000,1000,1000,1000,1000,5,2,0];nnnMinimum = True;nStartProgram;nvar i : integer;ntemD : Double;nbeginntemD := 0;nfor i := 1 to n - 1 dontemD := temD + Dis[Cities[i],Cities[i+1]];nFunctionResult := temD + Dis[0,Cities[1]] + Dis[Cities[n],n+1];nend;nEndProgram;nNewCodeBlock"13.2 快捷代码 最短路径问题";nConstant n = 8;nParameters Cities(1:n)=[1,n,0];nMDataSet[1000];//默认元素为1000ni,j,Dis=n0 1 2n0 2 5n0 3 1n1 4 12n1 5 14n1 6 10n2 4 6n2 5 10n2 6 4n3 4 13n3 5 12n3 6 11n4 7 3n4 8 9n5 7 6n5 8 5n6 7 8n6 8 10n7 9 5n8 9 2nEndMDataSet;nMinFunction Dis[0,Cities[1]]+Sum(i=1:n-1)(Dis[Cities[i],Cities[i+1]])+ Dis[Cities[n],n+1];nnnNewCodeBlock"14 “ParVariable”可以定义多个缺失变量；";nNewCodeBlock"14.1 定义一个缺失变量";nTitle "缺少变量值的特殊拟合";nVariable x,y;nParVariable a=[0,2*pi];nSharedModel;nFunction x=r*(a-sin(a+b))*cos(b)+r*(1-cos(a*b))*sin(b);ny=r*(1-cos(a-b))*cos(b)-r*(a-sin(a*b))*sin(b);nRowData;n35,41,46,52,58,63,70,75,80,85,90,95;n32,33,33.5,33,32,30,28,25,21,17.5,13,9;nNewCodeBlock"14.2 定义多个缺失变量";nTitle "缺少变量值的特殊拟合";nVariable x,y;nParVariable a=[0,2*pi],aa=[0,2*pi];nSharedModel;nFunction x=r*(a+aa-sin(a+aa+b))*cos(b)+r*(1-cos(a*b))*sin(b);ny=r*(1-cos(a+aa-b))*cos(b)-r*(a-sin(a*b))*sin(b);nRowData;n35,41,46,52,58,63,70,75,80,85,90,95;n32,33,33.5,33,32,30,28,25,21,17.5,13,9;