Model ValidationMany possible choices, no universally accepted paradigm. Some classical possibilities:Prediction error b
Model Validation
Many possible choices, no universally accepted paradigm. Some classical possibilities:
- Prediction error based criteria (CV).
- Information criteria (AIC, BIC, etc.).
- Mallow’s Cp statistic.
Before looking at these, let's introduce terminology: suppose that the true model is 



- The true model contains only the columns for which
.
- A correct model is the true model plus extra columns.
- A wrong model is a model that does not contain all the columns of the true model.
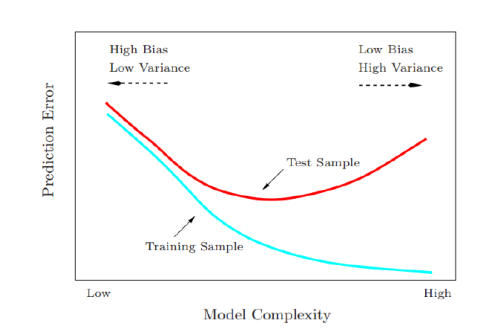
Test and training error as a function of model complexity:
- The training error tends to decrease whenever we increase the model complexity, that is , whenever we fit the data harder.
- However, with too much fitting, the model adapts itself too closely to the training data, and will not generalize well (i.e., have large test error).
Cross-validation: evaluating estimator performance.
Learning the parameters of a prediction function and testing it on the same data is a methodological mistake: a model that would just repeat the labels of the samples that it has just seen would have a perfect score but would fail to predict anything useful on yet-unseen data.
The estimator of the prediction error will be

In practice n is small and we cannot afford to split the data. Instead we use the leave-one-out cross validation sum of squares:

where 

so the full regression may be used. Alternatively, one may use a more stable version:

where “G” stands for “generalized”. It holds that

Suggests strategy: pick variables that minimize (G)CV.