10 聚类

发布时间：2023-06-14 19:45:34

聚类 (Clustering)以下内容基于周志华老师的机器学习第9章归纳整理。1 聚类任务无监督学习(Unsupervised Learning)就是在样本标

聚类 (Clustering)

以下内容基于周志华老师的机器学习第9章归纳整理。

1 聚类任务

无监督学习(Unsupervised Learning)就是在样本标签未知时，研究数据内在性质及规律的学习。其中应用最多的是聚类(clustering)。

2 性能度量

与监督学习相同，我们需要通过某种性能度量来评估聚类结果好坏。直观的讲，我们希望物以类聚。就是同一簇尽可能相似，不同簇尽可能不同。也就是说，簇内相似度(intra-cluster similarity)高且簇间相似度(inter-cluster similarity)低。

聚类的性能度量大致有两类。

一类是将结果与某个参考模型比较，称为外部指标(external index) - Jaccard系数(Jaccard Coefficient, JC) - FM指数(Fowlkes and Mallows Index, FMI) - Rand指数(Rand Index, RI)

上述度量结果均在[0,1]之间，越大越好。

另一类是不利用任何参考模型，称为内部指标(internal index) - DB指数(Davies-Bouldin Index, DBI) - Dunn指数(Dunn Index，简称DI)

DBI越小越好，而DI则越大越好。

此处不再复写书上的内容，因为根据笔者在文本方面的实战经验，大多数指标仅仅是理论可行。首先，海量短文本聚类，没有标签。标注也不可能，所以外部指标行不通。其次，指数为0.55的结果是否一定比0.51的好呢？技术上最好，也许业务上完全行不通，自己都觉得怪怪的，更没法跟业务人员解释。

这里贴一个笔者刚刚发现的CSDN相关文章，或许实用性更强，有待研究。

3 距离计算

距离度量需要满足非负性，同一性，对称性和传递性。

对于有序属性，最常用的是闵可夫斯基距离(Minkowski distance)：

容易看出，p=1即为曼哈顿距离。p=2即为欧式距离。

无序属性可采用VDM(Value Difference Metric)：

两者混合即可处理混合属性。

4 原型聚类

4.1 k均值算法(K-means)

K-means几乎是聚类方法中最经典的方法了。具体算法如下：

Pros CSDN

原理比较简单，实现也是很容易，收敛速度快
聚类效果较优
算法的可解释度比较强
主要需要调参的参数仅仅是簇数k

Cons

K值的选取不好把握(改进：可以通过在一开始给定一个适合的数值给k，通过一次K-means算法得到一次聚类中心。对于得到的聚类中心，根据得到的k个聚类的距离情况，合并距离最近的类，因此聚类中心数减小，当将其用于下次聚类时，相应的聚类数目也减小了，最终得到合适数目的聚类数。可以通过一个评判值E来确定聚类数得到一个合适的位置停下来，而不继续合并聚类中心。重复上述循环，直至评判函数收敛为止，最终得到较优聚类数的聚类结果)
对于不是凸的数据集比较难收敛(改进：基于密度的聚类算法更加适合，比如DESCAN算法)
如果各隐含类别的数据不平衡，比如各隐含类别的数据量严重失衡，或者各隐含类别的方差不同，则聚类效果不佳
采用迭代方法，得到的结果只是局部最优
对噪音和异常点比较的敏感(改进1：离群点检测的LOF算法，通过去除离群点后再聚类，可以减少离群点和孤立点对于聚类效果的影响；改进2：改成求点的中位数，这种聚类方式即K-Mediods聚类（K中值）)
初始聚类中心的选择(改进1：k-means++;改进2：二分K-means，相关知识详见这里和这里)

Code Sklearn

from sklearn.cluster import KMeansnkmeans = KMeans(n_clusters=2, random_state=0).fit(X)nkmeans.labels_nkmeans.cluster_centers_

4.2 高斯混合聚类(Gaussian Mixture Model, GMM)

采用概率模型来表达聚类原型。这里再次涉及到大量推导，戳知乎

5 密度聚类

基于密度的聚类(density-based clustering)假设聚类结构能通过样本分布的紧密程度确定。代表算法是DBSCAN(Density-Based S-patial Clustering of Applications with Noise)。

该算法定义的一个簇为由密度可达关系导出的最大密度相连样本集合。

原理详情戳简书

Code Sklearn

from sklearn.cluster import DBSCANnclustering = DBSCAN(eps=3, min_samples=2).fit(X)nclustering.labels_

Pros Aandds Blog

相比K-means算法和GMM算法，DBSCAN算法不需要用户提供聚类数量。
DBSCAN能分辨噪音点，对数据集中的异常点不敏感。

Cons

如果样本集的点有不同的密度，且该差异很大，这时DBSCAN将不能提供一个好的聚类结果，因为不能选择一个适用于所有聚类的 (ϵ,MinPts) 参数组合。注：OPTICS（Ordering Points To Identify the Clustering Structure）是DBSCAN算法的变种，它能较好地处理样本密度相差很大时的情况。
它不是完全决定性的算法。某些样本可能到两个核心对象的距离都小于 ϵ ，但这两个核心对象由于不是密度直达，又不属于同一个聚类簇，这时如何决定这个样本的类别呢？一般来说，DBSCAN采用先来后到，先进行聚类的类别簇会标记这个样本为它的类别。注：可以把交界点视为噪音，这样就有完全决定性的结果。

6 层次聚类(Hierarchical clustering)

层次聚类试图在不同层次对数据集进行划分，形成树形聚类结构。划分可采用自底向上的策略，也可以采用自顶向下的策略。

AGNES(AGglomerative NESting)是一种自底向上的算法。它先将每个样本看作一个初始聚类簇，然后每一步找寻最近的两个簇进行合并。不断重复直到预设聚类数。

数据量小的时候，笔者还是很喜欢该类算法的，因为生成的树状图(dendrogram)很好看：

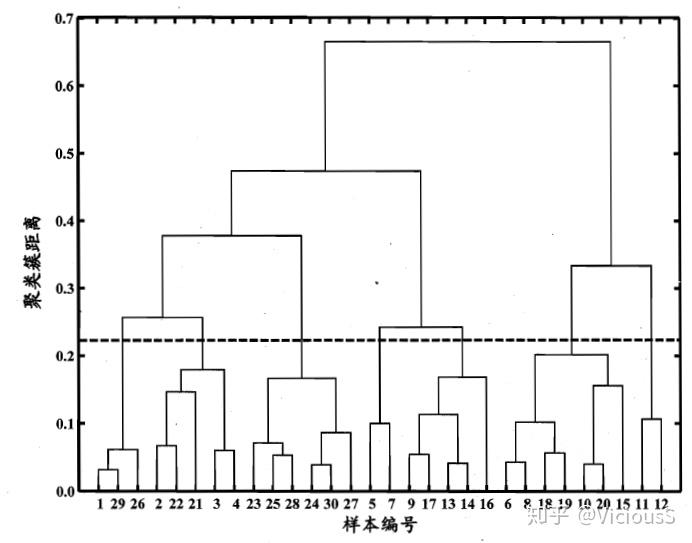
可惜数据量大的时候就只剩下密密麻麻的直线了。

Code Stackabuse

from scipy.cluster.hierarchy import dendrogram, linkagenfrom matplotlib import pyplot as pltnnlinked = linkage(X, 'single')nnlabelList = range(1, 11)nnplt.figure(figsize=(10, 7))ndendrogram(linked,n orientation='top',n labels=labelList,n distance_sort='descending',n show_leaf_counts=True)nplt.show()

面试问题

描述K均值算法 Describe the k-means algorithm.
什么是高斯混合模型 What is the Gaussian Mixture Model?
对比高斯混合模型和高斯判别分析 Compare Gaussian Mixture Model and Gaussian Discriminant Analysis.