剔除集合中过大过小的异常值
一个集合X中可能存在过大或过小的异常值,希望计算一个范围,剔除集合X中过大或过小的异常值,这个范围的上下限就是阈值,较大值称为阈值
一个集合X中可能存在过大或过小的异常值,希望计算一个范围,剔除集合X中过大或过小的异常值,这个范围的上下限就是阈值,较大值称为阈值上限,记为threshold_up,较小值称为阈值下限,记为threshold_down。
X=[x1,x2,…,xn]
算法原理
集合中只有少数是异常值,如果把X中的点看作空间中的点,则某个点距离其他点都很远时认为该点是异常值,正常值取值范围就是正常值中最小值到最大值的范围。
计算过程
1. 计算每个xi与其他所有值的绝对差的和,称为半径,记为R。
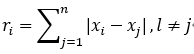
其中ri是半径序列R的第i个元素。
2. 记录下R中的元素从小到大排序后的索引序列,记为R_psort。
3. 最小半径min_r和最大半径max_r
min_r=RR_psort(1)
max_r= RR_psort (-1)
其中R_psort(1)是R_psort序列中的第一个(同R_psort1),R_psort(-1) 是R_psort序列中的最后一个。
4. 如果max_r比min_r大一个数量级(max_r≥min_r*10)则把大于min_r*5以上的半径对应的xi剔除。
(1) 大于min_r*5的索引min_r5_pos
min_r5_pos=j,RR_psort(j)≥min_r*5
(2) 按索引剔除X序列中的数,得到X_new
X_new=XXR_psort(j≥min_r5_pos)
其中R_psort(j≥min_r5_pos)是R_psort中所有不小于min_r5_pos的索引集合。
(3) 用X_new重复1,2,3,4,直到不满足max_r≥min_r*10。
5. 设最小半径的倍数为n(默认n=2,n≤5),称为半径倍数,找到半径大于min_r*n的索引min_rn_pos
min_rn_pos= j,RR_psort(j)>min_r*n
6. min_rn_pos之前的xi为正常值序列,称为阈值序列,记为X_normal
X_normal=XR_psort (j≤min_rn_pos-1)
7. 计算阈值上下限threshold_up和threshold_down
threshold_up= max(X_normal)
threshold_down= min(X_normal)
写出代码:
| A | B | C | D | |
| 1 | =seq | /集合X | ||
| 2 | =up_down | /上限或下限 | ||
| 3 | =n | /半径倍数n | ||
| 4 | =func(A7,seq,up_down,n) | |||
| 5 | return A4 | /返回结果 | ||
| 6 | /计算阈值,参数:序列,上限或下限,半径 | |||
| 7 | func | |||
| 8 | =if(B7=="up",func(A10,A7,C7),func(A15,A7,C7)) | /如果取上限就取阈值序列的最大值,下限就取阈值序列的最小值 | ||
| 9 | /计算阈值上限 | |||
| 10 | func | |||
| 11 | =A10.select(~) | /过滤 null | ||
| 12 | if B11==[] | return null | ||
| 13 | =func(A20,B11,B10).max() | /X_normal.max() | ||
| 14 | /计算阈值下限 | |||
| 15 | func | |||
| 16 | =A15.select(~) | /过滤 null | ||
| 17 | if B16==[] | return null | ||
| 18 | =func(A20,B16,B15).min() | / X_normal.min() | ||
| 19 | /计算阈值序列,参数:序列,半径倍数 | |||
| 20 | func | |||
| 21 | =A20.((v=~,A20.(abs(v-~))).sum()) | /R | ||
| 22 | =B21.psort() | /R_psort | ||
| 23 | if B21(B22(1))*10<B21(B22.m(-1)) | =B22.pselect(B21(~)>=B21(B22(1))*5) | /如果 max_r>min_r*10min_r5_pos | |
| 24 | =A20(A20(B22.m(C23:))) | /去掉大于 min_r*5 的值 | ||
| 25 | return func(A20,C24,B20) | |||
| 26 | else | =B21(B22(1))*B20 | /min_r*n | |
| 27 | =(gt_min=B22.pselect(B21(~)>C26),if(!gt_min,A20.len(),gt_min-1)) | /min_rn_pos | ||
| 28 | =A20(B22.to(C27)) | /X_normal |
输入参数说明:
1. A1中的seq是输入集合X;
2. A2中的up_down是计算上限还是下限的参数。
up_down=“up”时,计算阈值上限;
up_down=“down”时,计算阈值下限。
3. A3中的n是半径倍数n;
2≤n≤5
n越大正常值的取值范围越大,即阈值上限越大,阈值下限越小。
算法效果实例
1. 把集合X和不同半径倍数n条件下的阈值上下限画在图上如下:

图中横轴是每个值的索引,纵轴是X中值的大小。图右侧的图例说明
X:集合X
X_n2_up:n=2时的阈值上限
X_n2_down:n=2时的阈值下限
X_n2.5_up:n=2.5时的阈值上限
X_n2.5_down:n=2.5时的阈值下限
X_n3_up:n=3时的阈值上限
X_n3_down:n=3时的阈值下限
不大于阈值上限且不小于阈值下限的值就是X中的正常值。
http://www.raqsoft.com.cn/wx/course-data-mining.html









