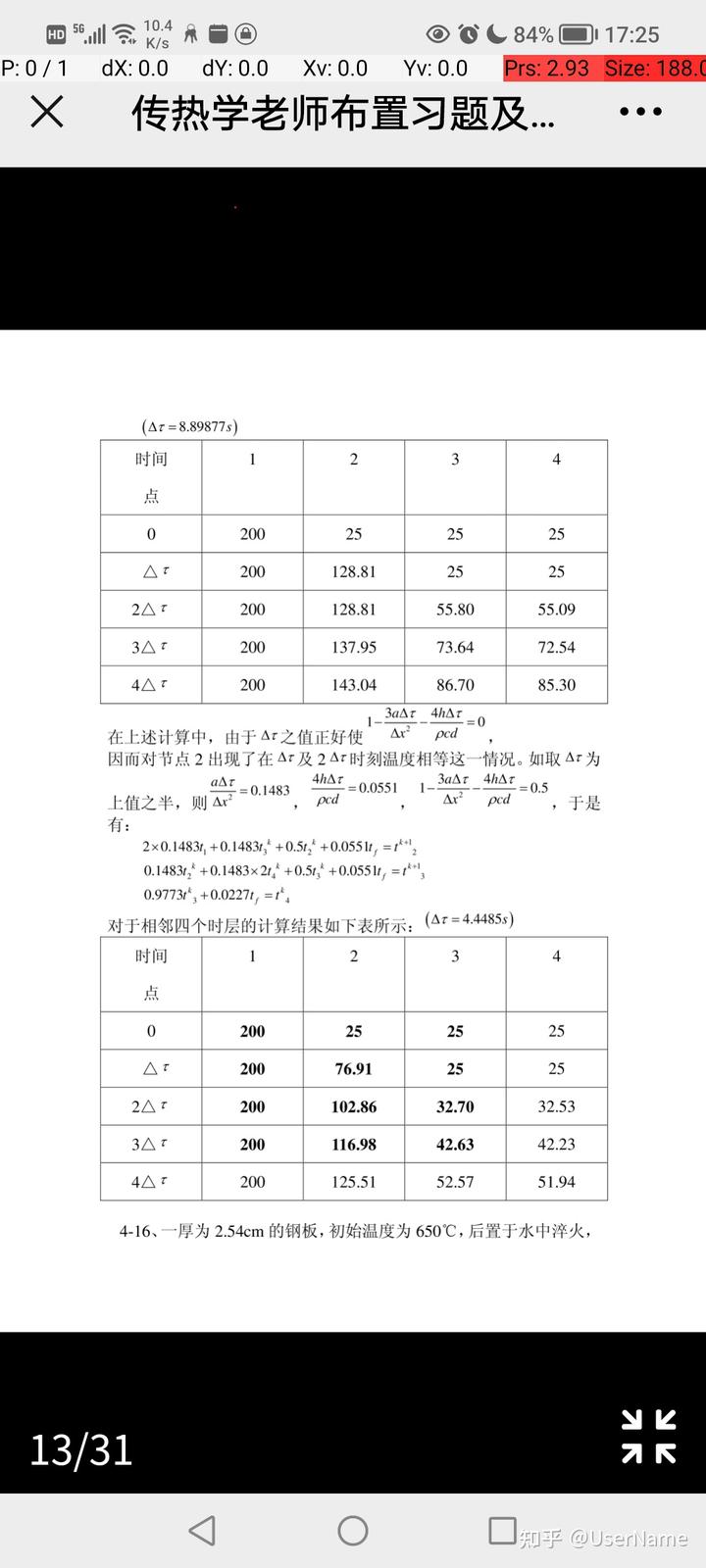
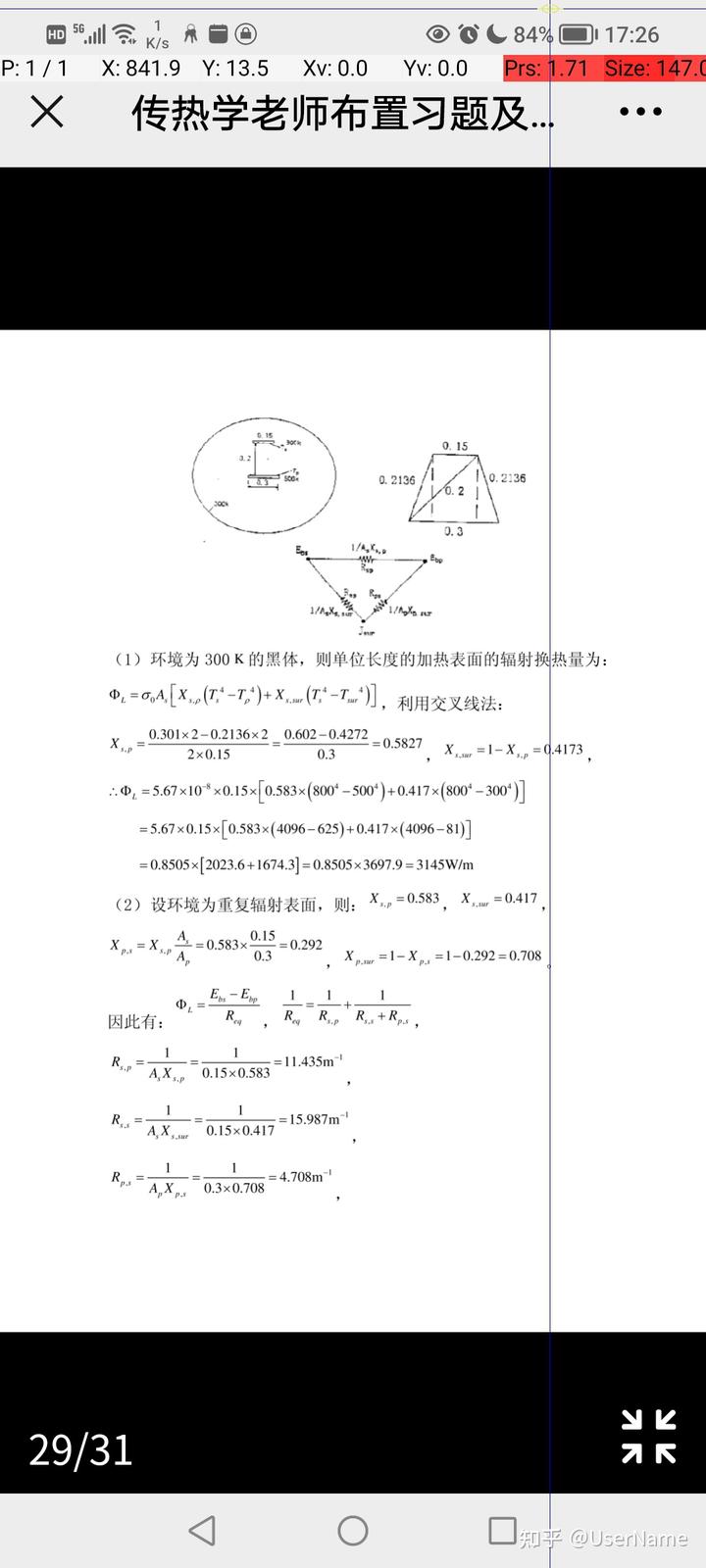
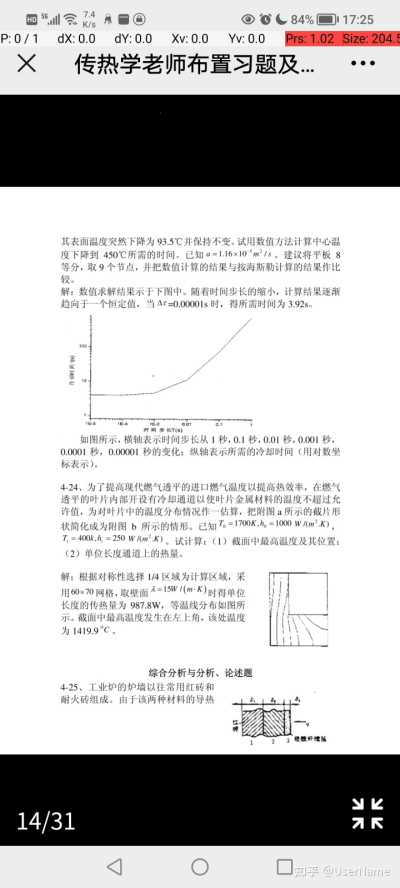
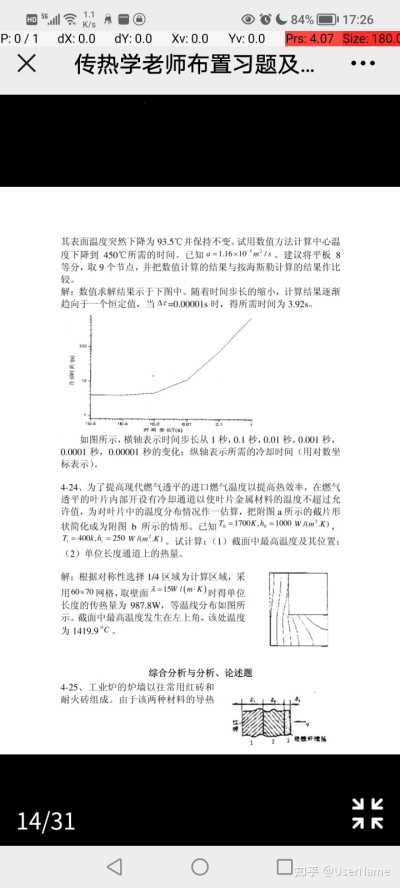
online open-source test

42.3H田56，l令K/s0C84％□117：25P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.79Size:188.×传热学老师布置习题及……1-4对于附图所示的两种

42.3H田56，l令K/s0C84％□117：

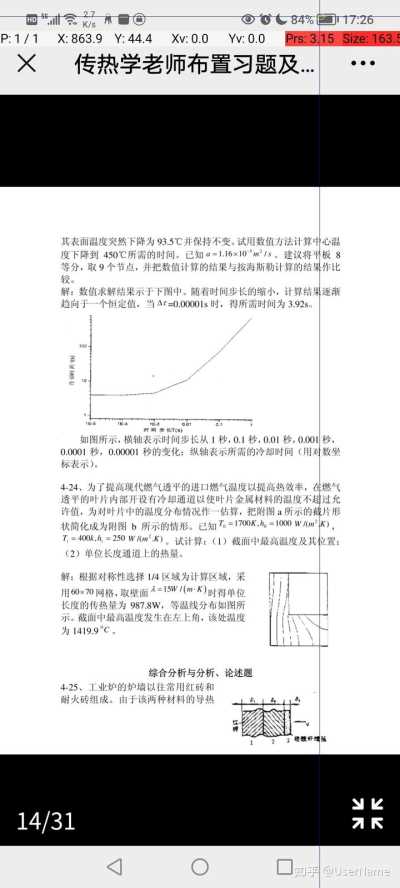
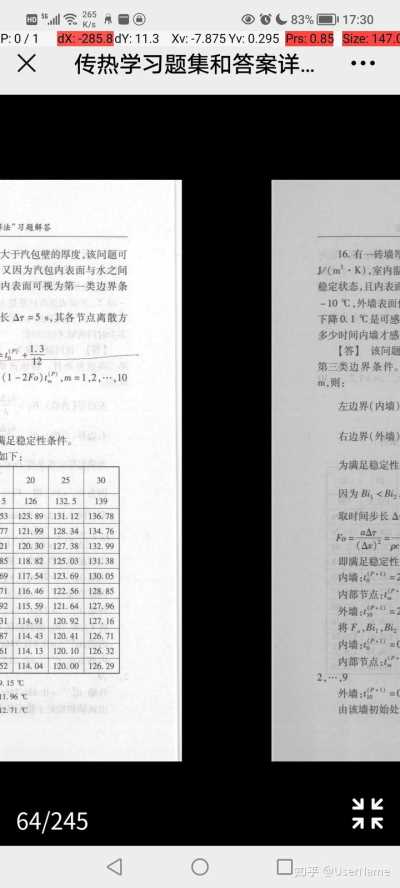
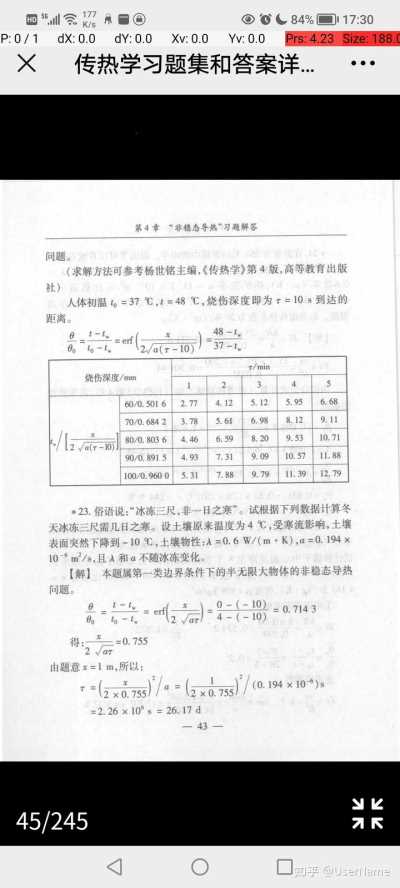
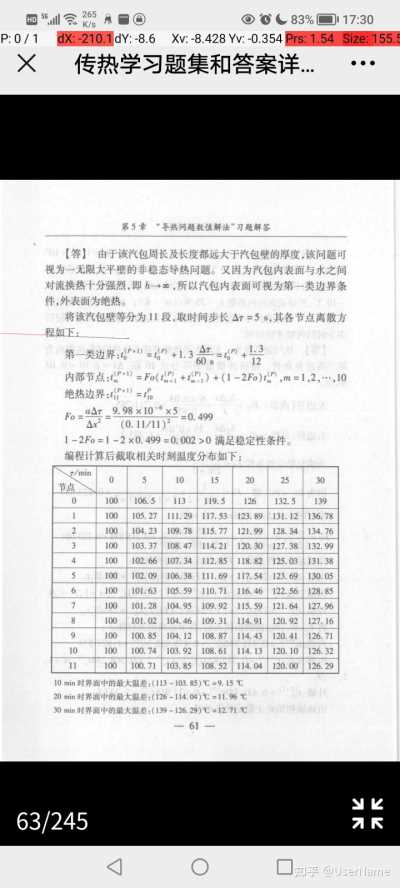
25P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.79Size:188.×传热学老师布置习题及……1-4对于附图所示的两种水平夹层，试

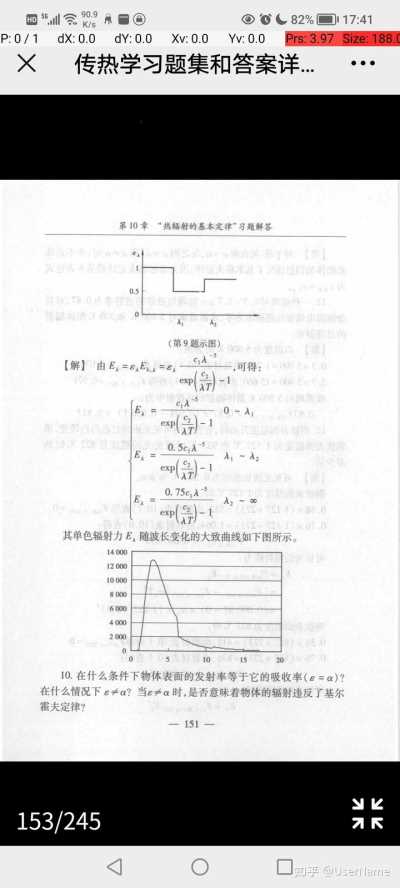
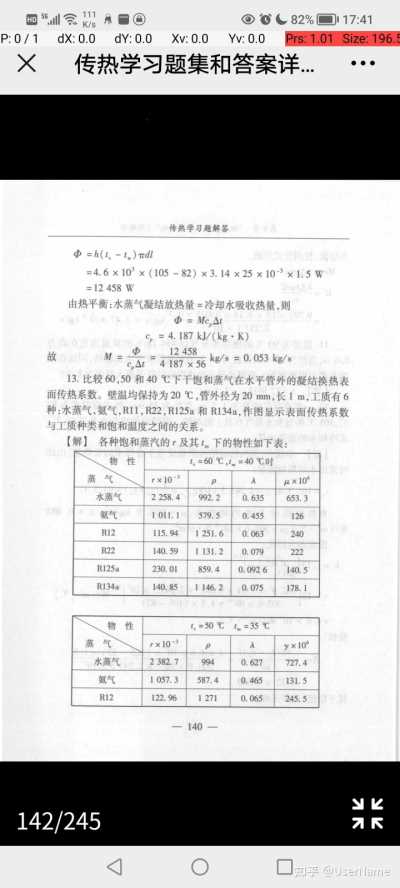
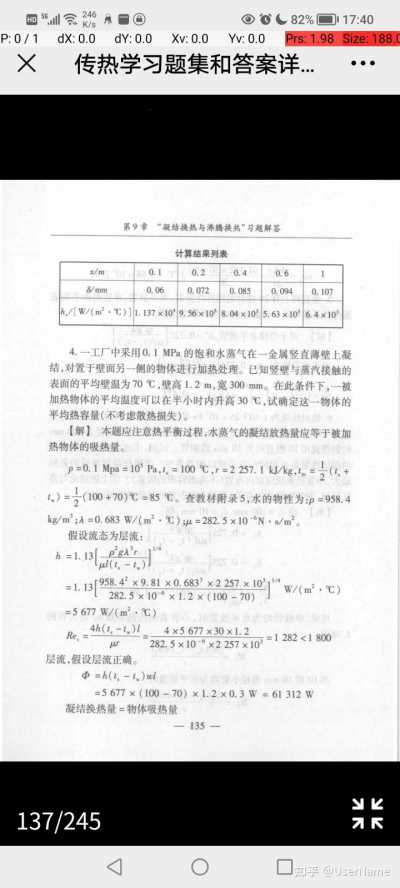
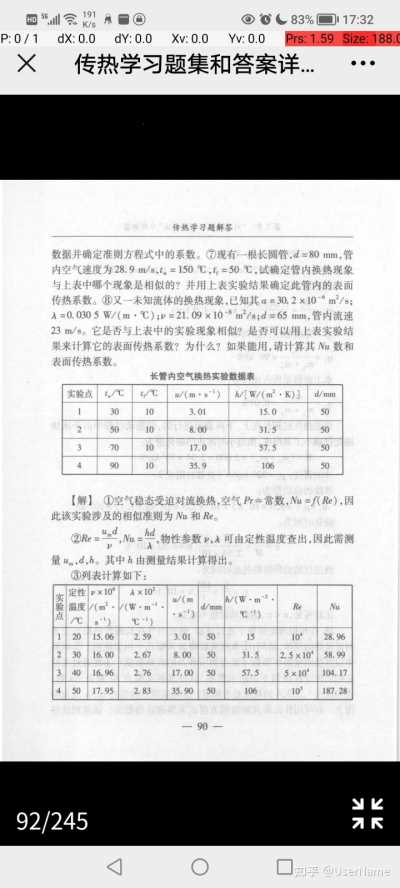
分析冷、热表面间热量交换的方式有何不同？如果要通过实验来测定夹层中流体的导热系数，应采用哪一种布置？解：（a）中热量交换的方式主要为热传导。（b）热量交换的方式主要有热传导和自然对流。所以如果要通过实验来测定夹层中流体的导热系数，应采用（a）布置。1-9一砖墙的表面积为12m2，厚为260mm，平均导热系数为1.5W/（m.K）。设面向室内的表面温度为25℃，而外表面温度为-5℃，试确定次砖墙向外界散失的热量。解：根据傅立叶定律有：中＝A41＝1.5×12x25-（-）5＝2076.9W0.261-27设冬天室内的温度为＇，室外温度为＇2，试在该两温度保持不变的条件下，画出下列三种情形从室内空气到室外大气温度分布的示意性曲线：（1）室外平静无风；（2）室外冷空气以一定流速吹过砖墙表面：（3）除了室外刮风以外，还要考虑砖墙与四周环境间的辐射换热。解1-32一玻璃窗，尺寸为60cm×30cm，厚为4mm。冬天，室内及室外温度分别为20℃及-20℃，内表面的自然对流换热表面系数为W，外表面强制对流换热表面系数为50W（m.K）。玻璃的导热系数＝0.78W（m.K）。试确定通过玻璃的热损失。1/31口6H四56，l令K0084％117:25P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.57Size:171.×传热学老师布置习题及……△T0＝11＋6解：hAAh2A＝57.5W2-9双层玻璃窗系由两层厚为6mm的玻璃及其间的空气隙所组成，空气隙厚度为8mm。假设面向室内的玻璃表面温度与室外的玻璃表面温度各为20℃及-20℃，试确定该双层玻璃窗的热损失。如果采用单层玻璃窗，其他条件不变，其热损失是双层玻璃的多少倍？玻璃窗的尺寸为60cm×60cm。不考虑空气间隙中的自然对流。玻璃的导热系数为0.78W/（m.K）。t1-t29＝882392＝12＝5200w/m6解：么名么3＝116.53W/m2∴Q＝Ag＝41.95W92-5200＝44.62所以41116.532-13在附图所示的平板导热系数测定装置中，试件厚度δ远小于直径d。由于安装制造不好，试件与冷热表面之间平均存在着一层厚为△＝0.1mm的空气隙。设热表面温度4＝180℃，冷表面温度2＝30℃，空气隙的导热系数可分别按，2查取。试计算空气隙的存在给导热系数测定带来的误差。通过空气隙的辐射换热可以略而不计。解：查附表8得4＝180℃，＝3.72x102W/m.K）；t2＝30℃，2＝2.67×102W1（m.K）；①＝1-12A＝180-30、d264无空气时:6＝0.029315名，＝34.328有空气隙时t，一t2＝2＋-A得＝43.988-＝28.1所以相对误差为圆筒体2/31四川盒3.4K/s⊙084％117：25P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.02Size:188.×传热学老师布置习题及……2-17一蒸汽锅炉炉膛中的蒸发受热面管壁受到温度为1000℃的烟气加热，管内沸水温度为200℃，烟气与受热面管子外壁间的复合换热表面传热系数为100W/（m2.K），沸水与内壁间的表面传热系数为5000W/（m2.K），管壁厚6mm，管壁＝42W/（m.K），外径为52mm。试计算下列三种情况下受热面单位长度上的热负荷：（1）换热表面是干净的：（2）外表面结了一层厚为1mm的烟灰，其＝0.08W/（m.K）；（3）内表面上有一层厚为2mm的水垢，其＝1W1（m.K）。解：（1）中＝2d（1-t2）2π×1（1000-200）1n（r2/r）11In（52/40），1-＝12532.98Whh225000×0.02420.026x1002r（t，-t，）p＝1n（％1r）n（r，r）＋1hroo2π×1（1000-200）＝5852.94W1，ln（54/52），ln（52/40，1（2）0.02×50000.08420.027×100（3）中＝2d（1-t2）1In（r/2）In（2/）In（/）1hrooAAhori2π×1（1000-200）＝5207.06W1，n（54/52），ln（52/40），ln（40/36），15000×0.0180.08421100×0.0272-20一直径为d长为1的圆杆，两端分别与温度为4及2的表面接触，杆的导热系数为常数。试对下列两种情形列出杆中温度的微分方程式及边界条件，并求解之：杆的侧面是绝热的；杆的侧面与四周流体间有稳定的对流换热，平均表面传热系数为h，流体温度＇小于及2。otnd2a1＋解：①＝-a4，中2＝-2a4，在侧面绝热时，有＝多02t得微分方程为：x2，边界条件为：x＝0，1＝1x＝1，1＝t212-x＋t1解微分方程得：3/31口HD56，l令3.4K/s084％□17：25P:0/1dX:-4.0dY:2.0Xv:0.0Yv:0.0Prs:1.14Size:171.×传热学老师布置习题及……2＝nddxh（t-ty），根据条件有：4＝2＋02t4ht-t）＝0得微分方程为：ax2da，边界条件为：x＝0，t＝tx＝l，t＝t2（2.解微分方程得：1-t＝C＋Ce“代入边界条件得：（t2-t）-（1-t，）et-tr（1-1）-（2-1）2-34设一平板厚为6，其两侧表面分别维持在温度4及2。在此温度范围内平板的局部导热系数可以用直线关系式（1）＝（1＋b1）来表示。试导出计算平板中某处当地热流密度的表达式，并对b＞O，b＝0及b＜0的三种情况画出温度分布的示意曲线。2-53过热蒸气在外径为127mm的钢管内流过，测蒸气温度套管的布置如附图所示。已知套管外径d＝15mm，壁厚6＝0.9mm，导热系数＝49.1W/（m.K）。蒸气与套管间的表面传热系数h＝105W/（m2.K）。为使测温误差小于蒸气与钢管壁温度差的0.6％，试确定套管应有的长度。解：按题意应使0n/0o≤0.6％，0n/0＝1/ch（mh）＝0.6/100，ch（mh）＝166.7，查附录得：mh＝arclch（166.7）＝5.81，hU105mV4，V49.1x0.9x10＝48.75，H5.81＝0.119m48.752-76刚采摘下来的水果，由于其体内葡萄糖的分解而具有“呼吸”作用，结果会在其表面析出CO2，水蒸气，并在体内产生热量。设在通风的仓库中苹果以如附图所示的方式堆放，并有5℃的空气以0.6m/s的流速吹过。苹果每天的发热量为4000J/kg。苹果的密度p＝840kg/m3，导热系数＝0.5W1（m.K）；空气与苹果间的表面传热系数h＝6W（m2.K）。试计算稳态下苹果表面及中心的温度。每个苹果可按直径为80mm的圆球处理。21020t＋＝0解：利用有内热源的一维球坐标方程：“r2r（r＝-r2o12r2d＝-r3dr31＋-＋号＋C1＋C2人4/31口H田56l令K/s2.10C84％□17：25P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.41Size:196.×传热学老师布置习题及……r＝0，a边界条件为：or0.r＝R-＝（-）为满足第一边界条件，c必须为0。代入第二条件：，即，OROR2由此得：2＝3h＋6＋1中R，中）＝3n（R2-r2）＋t温度分布为：ROROR2由此得：当r＝R时，3h＋h；当r＝0时，6＝3h62＋too3P3＝4nR2h（-1）R1，也可由稳态热平衡得出：由此得：3h，市＝4000J/（m3day）＝4000J4000J＝38.9W/m31.190×10-3m3×24×3600s102.8m2s1，＝5℃＋R＝5C＋8.9m3＊0.04m＝5℃＋0.086℃＝5.09℃3h3x6W/（m2K）38.9×0.04℃1o＝5℃＋OROR2＝5.09＋＝5.09＋0.02＝5.11℃3h6A6×0.53一1设有五块厚30mm的无限大平板，各用银、铜、钢、玻璃及软木做成，初始温度均匀（20℃），两个侧面突然上升到60℃，试计算使用中心温度上升到56℃时各板所需的时间。五种材料的热扩散依次为170×10-m2/s、103×10-m2/s，12.9×106m2/s、0.59×10-m2/s及0.155×106m2/s。由此计算你可以得出什么结论？解：一维非稳态无限大平板内的温度分布如下函数关系式：0t-to＝f（Bi，Fo，0too-t0不同材料的无限大平板，均处于第一类边界条件（即Bi→∞）。由题意知材料达到同样工况式Bi数和x/6相同，要使温度分布相同，则只需Fo数相同5/31H田56l令K/s5.90C84％□17：25P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:2.04Size:179.×传热学老师布置习题及……学）二（学），而相等因此，（Fo）1＝（Fo）2，即故知a小所需时间大a铜＞a银＞钢＞0玻璃＞a软本所以T钢＜T银＜T钢＜T玻璃＜T软术。3一6一初始温度为to的物体，被置于室温为t的房间中。物体表面的发射率为￡，表面与空气间的换热系数为h。物体的体集积为V，参数与换热的面积为A，比热容和密度分别为c及P。物体的内热阻可忽略不计，试列出物体温度随时间变化的微分方程式。解：由题意知，固体温度始终均匀一致，所以可按集总热容系统处理固体通过热辐射散到周围的热量为：91＝0A（T-TA）固体通过对流散到周围的热量为：92＝hA（T-T）固体散出的总热量等于其焓的减小91＋92＝-PCdd即A（T-T）＋hA（T-T）＝-pc43一15一种火焰报警器采用低熔点的金属丝作为传热元件，当该导线受火焰或高温烟气的作用而熔断时报警系统即被触发，一报警系统的熔点为500℃，＝210w（m·K），p＝7200kg/m3，c＝420J（kg·K），初始温度为25℃。问当它突然受到650℃烟气加热后，为在1min内发生报警讯号，导线的直径应限在多少以下？设复合换热器的表面换热系数为12W/（m2·K）。解：采用集总参数法得：6/31口HD56，l令5.9K/s⊙0C84％□17：25P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.07Size:188.×传热学老师布置习题及……旦＝exp（hA）％pcv，要使元件报警则x≥500C500-650＝exp（hA入25-650Pcv，代入数据得D＝0.669mm验证Bi数：h（V/A）hDBi＝＝0.0095×103＜0.0542，故可采用集总参数法。3一21有两块同样材料的平板A及B，A的厚度为B的两倍，从统一高温炉中取出置于冷流体中淬火。流体与各表面间的表面传热系数均可视为无限大。已知板B中心点的过余温度下降到初值的一半需要20min，问A板达到同样温度工况需要的时间？解：BiA＝Big＝o→0m＝f（Fo）＝0.5→F0A＝F0aA＝ag6A＝26→TA（②）2t＝48＝4x20min＝80min3-54、已知：一正方形人造木块，边长为0.1m，＝0.65W/（m·K），p＝810kg/m3，c＝2550J1（kg·K），初温为25℃，1＝425C，h＝6.5W/m2·K），经过4小时50分24秒后，木块局部地区开始着火。求：此种材料的着火温度。解：木块温度最高处位在角顶，这是三块无限大平板相交处。7/31H田56，l令K/s4.8⊙084％□17：25P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.83Size:180.×传热学老师布置习题及……h86.5×0.05Bi＝＝0.5＞0.1；由图3-7查得＝0.80.6520.65a＝＝3.147×10-7m2/s，F。＝a_3.147×10-7×17424＝2.19:Pc810×2550R20.052由图3-6查得＝0.4.＝0.8×0.41＝0.328.0o000角顶处无量纲温度：日＝（）＝0.3283＝0.0353，0∴角顶温度：t＝t＋0.0353（t。-t）＝425＋0.0353×（25-425）＝411C.3-5、己知：一易拉罐饮料，初温为30C，物性可按水处理，的直径为50m，高为120m罐壳的热阻可以忽略，罐中的饮料的自然对流可以忽略。t＝5Ch＝10W/（m2.K）.求：饮料到达10C所需的时间。30＋10＝20°C解：物性按2计，则有x＝0.599W/（m·K），a＝14.3×10-m2/s，h610×0.06hR10×0.025B1＝20.599＝1.002，B，＝1.0，B。＝x＝0.599＝0.417，B＝2.4.0＝30-5＝25C，0＝10-5＝5°C5＝0.2.9＝Aci00250％对平板：P＝（a＋B））1＝（0.40220.91881＝0.75801.0021A＝a＋b（1-ecBi）＝1.0101＋0.2575（1-e-0427x102）＝1.0998，8＝30-5＝25C，0＝10-5＝5C，＝5＝0.2，0＝Ae，0％2500对柱体：2＝（a＋上）1＝（0.1700＋0.4349B0.417）-＝0.8245，A＝a＋b（1-ei）＝1.0042＋0.5877（1-e04238x0417）＝1.0953，at＝a，62＝0.062＝0.0036，R2＝0.0252＝0.000625.Fop＝，Fo，＝R2，x0.0036＝5.76F0p于是有：F0，＝Fopx0.000625（m）（）＝1.2046e0.0。＇0.2＝51＝0.1660-1.7856＝-5.5071FF0＝0.324，1.2046＝0.324×0.062/（14.3x10-8）＝8162.65s＝2.27h.8/31HD56l令8.6K/sC84％C□17：25P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.64Size:188×传热学老师布置习题及……4-3、试对附图所示的常物性，无内热源的二维稳态导热问题用高斯-赛德尔迭代法计算，t2，t3，t4之值。解：温度关系式为：［1＝1/4（t2＋t3＋40＋30）12＝1/4（1＋14＋20＋30）13＝1/4（11＋14＋30＋15）14＝1/4（12＋13＋10＋5）（0）开始时假设取＝0＝20℃；9＝0＝15℃得迭代值汇总于表迭代次数20201515126.2522.812521.562514.84375228.5937523.35937522.10937515.1171875328.867187523.4960937522.2460756515.18554258428.9355425823.5302712922.2802712915.20263565528.9526356523.5388178222.288817825.20690891628.956908923.5409544622.29095544515.20797723其中第五次与第六次相对偏差已小于10迭代终止。4-5、试将直角坐标中的常物性无内热源的二维稳态导热微分方程化为显式差分格式，并指出其稳定性条件（△r≠4y）。解：常物性无内热源二维非稳态方程微分方习题4-4附图程为0t_02t，a2tax2ay2扩散项取中心差分，非稳态项取向前差分：t（）--2t＋t-2＋t△T△x2△y2所以有9/31H田56l令K/s5.7084％□117：25P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.06Size:171.×传热学老师布置习题及……-＋m1200稳定性条件F0A＋F0Ay≤1/24-9、在附图所示的有内热源的二维导热区域中，一个界面绝热，一个界面等温（包括节点4），其余两个界面与温度为＇的流体对流换热，h均匀，内热源强度为中。试列出节点1，2，5，6，9，10的离散方程式。解：节点1：节点2：＋（）＋2（＋00＝0节点5：＋2（＋2-（）＋00--1）＝0节点6：）＋25-（）＋2-1（）＋25-（）-0＝0节点9：2（）＋20（）＋4（）-1）-0节点10-10△x1＋-0（＋2-1-W（-1）＝0当Ar＝Ay以上诸式可简化为：ts＋t2节点1：（），-2（22）＋40（）＝0节点2：26＋＋3-＋19）＝021＋1＋1g＋2节点5：）-2（2）＋0（）-0节点6：3＋0＋＋-4＋4（）＝0s＋t1o节点9：y-2（）＋240（）＝0节点10：20＋＋22）-2（20＋0（）＝010/31H56l令3.1K/s84％□17：25P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.0Size:188.×传热学老师布置习题及……4-10、一等截面直肋，高H，厚6，肋根温度为o，流体温度为，表面传热系数为h，肋片导热系数为。将它均分成4个节点（见附图），并对肋端为绝热及为对流边界条件（h同侧面）的两种情况列出节点2，3，4的离散方程式。设H＝45cm，6＝10mm，h＝50W/（m2.K），＝50W（m.K），o＝100℃，1＝20℃，计算节点2，3，4的温度（对于肋端的两种边界条件）。习题4-10附图解：采用热平衡法可列出节点2、3、4的离散方程为：a（1-12）82（13-12）8-2h△x（12-1）＝0节点2：△r△ra（12-13）8.2（4-13）8-2h△r（3-ty）＝0节点3：△Ara（13-14）8节点4：肋端绝热△r-h△x（a-1，）＝02（3-14）8肋端对流-h△x（4-t，）-h8（4-1，）＝0HAr其中3。将已知条件代入可得下列两方程组：肋端绝热3-2.045t2＋100.9＝0t2-2.04513＋t4＋0.9＝043-1.0225t4＋0.45＝0肋端对流t3-2.045t2＋100.9＝0t2-2.045t3＋t4＋0.9＝043-1.0375t4＋0.8＝0由此解得：肋端绝热2＝92.2C，13＝87.7C，14＝86.2C:肋端对流2＝91.5C，t3＝86.2C，14＝83.8C。肋端对流换热的条件使肋端温度更接近于流体温度。4-15、一直径为1cm，长4cm的钢制圆柱形肋片，初始温度为25℃，其后，肋基温度突然升高到200℃，同时温度为25℃的气流横向掠过3习题4～15附图11/313.1H田56l令K/s⊙084％□17：25P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.13Size:188.×传热学老师布置习题及……该肋片，肋端及两侧的表面传热系数均为100W/（m2.K）。试将该肋片等分成两段（见附图），并用有限差分法显式格式计算从开始加热时刻起相邻4个时刻上的温度分布（以稳定性条件所允许的时间间隔计算依据）。已知＝43W/（m.K），a＝1.333×103m2/s。（提示：节点4的离散方程可按端面的对流散热与从节点3到节点4的导热相平衡这一条件列出）。解：三个节点的离散方程为：节点2：（）心（）（a-r）-（节点3：△x12）2（）-5＝（（节点4：（）（）-）以上三式可化简为：2＝（）＋（器）＋3a△x4h△t△x2pcd州＝（）＋2（-）a＋4h3a△、4hA）ped，＋（t△x2pcd（2A＋△xh）t＂＝2ar3＋△xht，1_3a△_4h△T20△S1/稳定性要求△r2pcd，即元43pc＝a1.333×10＝32.258×105，代入得：3×1.333×10-54×100Ar＜1/＝8.89877s0.0220.01×32.258×1030.099975＋0.0124如取此值为计算步长，则：a△1.333×10-3×8.89877＝0.29664h△_4×100×8.89877＝0.1103△r20.022，pcd32.258×103×0.01于是以上三式化成为：2×0.29661＋0.29661，＋0.1103t，＝t＋20.2966t2＋0.2966×2t4＋0.1103t，＝tk＋0.9773，＊＋0.0227t，＝t12/31H田56l令K/s10.4084％117:25P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:2.93Size:188.×传热学老师布置习题及……（△＝8.89877s）时间1234点0200252525△200128.8125252△T200128.8155.8055.093△x200137.9573.6472.544△200143.0486.7085.3013a△t4h△t＝0在上述计算中，由于△t之值正好使△r2pcd因而对节点2出现了在△及2△时刻温度相等这一情况。如取△为a△t＝0.1483上值之半，则△r24AT-＝05511-304A＝0.5pcd△x2pcd，于是有：2×0.1483，＋0.148312k＋0.5t2＋0.0551，＝tk＋0.148312＋0.1483×214＋0.513＋0.0551，＝0.9773tk3＋0.02271，＝t＋对于相邻四个时层的计算结果如下表所示：（4＝4.4485s）时间1234点0200252525△T20076.9125252△200102.8632.7032.533△200116.9842.6342.234△200125.5152.5751.944-16、一厚为2.54cm的钢板，初始温度为650℃，后置于水中淬火，13/31H田56l令K/s7.4⊙C84％C□117：25P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.02Size:204.×传热学老师布置习题及……其表面温度突然下降为93.5℃并保持不变。试用数值方法计算中心温度下降到450℃所需的时间。已知a＝1.16x10m2/s。建议将平板8等分，取9个节点，并把数值计算的结果与按海斯勒计算的结果作比较。解：数值求解结果示于下图中。随着时间步长的缩小，计算结果逐渐趋向于一个恒定值，当△t＝0.00001s时，得所需时间为3.92s。100101E-51E41E30.010.1时间步长T（s）如图所示，横轴表示时间步长从1秒，0.1秒，0.01秒，0.001秒，0.0001秒，0.00001秒的变化；纵轴表示所需的冷却时间（用对数坐标表示）。4-24、为了提高现代燃气透平的进口燃气温度以提高热效率，在燃气透平的叶片内部开设有冷却通道以使叶片金属材料的温度不超过允许值，为对叶片中的温度分布情况作一估算，把附图a所示的截片形状简化成为附图b所示的情形。已知T＝1700K，hg＝1000W（m2.K），T，＝400k，h＝250W/（m2.K）。试计算：（1）截面中最高温度及其位置；（2）单位长度通道上的热量。解：根据对称性选择1/4区域为计算区域，采用60x70网格，取壁面2＝15W（m·K）时得单位长度的传热量为987.8W，等温线分布如图所示。截面中最高温度发生在左上角，该处温度为1419.9C。综合分析与分析、论述题4-25、工业炉的炉墙以往常用红砖和耐火砖组成。由于该两种材料的导热了建虾线14/31口H田56令2.9K/s⊙0C84％□17：25P:0/1dX:-117.0dY:513.5Xv:-1.911Yv:12.890Prs:0.86Size:171.×传热学老师布置习题及…解：（1）25℃的空气v＝15.53×106m2/sRe，＝ux1×x＝15.53×106＝5×103x＝7.765m（2）25℃的水v＝0.9055×106m2/sx＝0.45275m（3）14号润滑油v＝313.7×10-6m2/sx＝156.85m5-11、已知：如图，外掠平板的边界层的动量方程式为：ououa2u“ax＋yy2求：沿y方向作积分（从y＝0到y≥6）导出边界层的动量积分方程。解：任一截面做y＝0到y→的积分根据边界层概念y＞，u≈ua1＝0.yu0.2u0故在该处xy28Tudy＋ody-fd（1）其中。oy＂-o由连续行方程可得soudy，Vs二s.oudyoayoaxoaudy所以y，audy＋x。Ox（2）16/31H田56l令K/s2.9⊙084％□17：25P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:4.40Size:188×传热学老师布置习题及……解：（1）25℃的空气v＝15.53×106m2/sRe，＝ux1×x＝15.53×106＝5×103x＝7.765m（2）25℃的水v＝0.9055×106m2/sx＝0.45275m（3）14号润滑油v＝313.7×10-6m2/sx＝156.85m5-11、已知：如图，外掠平板的边界层的动量方程式为：ououo2uay2求：沿y方向作积分（从y＝0到y≥6）导出边界层的动量积分方程。解：任一截面做y＝0到y→的积分根据边界层概念y＞，u≈uu0.在该处xay2u＝0y2（1）其中oy＂-o由连续行方程可得00y＝-0oaysoudy，vs二s.oudyoaxudy＝-所以yaudy＋Jux。x（2）16/31H丽56llK/s2.7O084％D17:26P:1/1X:863.9Y:44.4Xv:0.0Yv:0.0Prs:3.15Size:163.×传热学老师布置习题及…其表面温度突然下降为93.5℃并保持不变。试用数值方法计算中心温度下降到450℃所需的时间。已知a＝1.16x10m2/s。建议将平板8等分，取9个节点，并把数值计算的结果与按海斯勒计算的结果作比较。解：数值求解结果示于下图中。随着时间步长的缩小，计算结果逐渐趋向于一个恒定值，当△t＝0.00001s时，得所需时间为3.92s。100101E-51E41E30.010.1时间步长T（s）如图所示，横轴表示时间步长从1秒，0.1秒，0.01秒，0.001秒，0.0001秒，0.00001秒的变化；纵轴表示所需的冷却时间（用对数坐标表示）。4-24、为了提高现代燃气透平的进口燃气温度以提高热效率，在燃气透平的叶片内部开设有冷却通道以使叶片金属材料的温度不超过允许值，为对叶片中的温度分布情况作一估算，把附图a所示的截片形状简化成为附图b所示的情形。已知T％＝1700K，h＝1000W（m2K），T，＝400k，h＝250W1（m2.K）。试计算：（1）截面中最高温度及其位置；（2）单位长度通道上的热量。解：根据对称性选择1/4区域为计算区域，采用60x70网格，取壁面2＝15W（m·K）时得单位长度的传热量为987.8W，等温线分布如图所示。截面中最高温度发生在左上角，该处温度为1419.9℃。综合分析与分析、论述题4-25、工业炉的炉墙以往常用红砖和耐火砖组成。由于该两种材料的导热了建数虾线监Y14/31口H四56，ll令K/s1.1⊙C84％C□17：26P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:4.07Size:180.×传热学老师布置习题及……其表面温度突然下降为93.5℃并保持不变。试用数值方法计算中心温度下降到450℃所需的时间。已知a＝1.16x10m2/s。建议将平板8等分，取9个节点，并把数值计算的结果与按海斯勒计算的结果作比较。解：数值求解结果示于下图中。随着时间步长的缩小，计算结果逐渐趋向于一个恒定值，当△t＝0.00001s时，得所需时间为3.92s。100101E-51E41E30.010.1时间步长T（s）如图所示，横轴表示时间步长从1秒，0.1秒，0.01秒，0.001秒，0.0001秒，0.00001秒的变化；纵轴表示所需的冷却时间（用对数坐标表示）。4-24、为了提高现代燃气透平的进口燃气温度以提高热效率，在燃气透平的叶片内部开设有冷却通道以使叶片金属材料的温度不超过允许值，为对叶片中的温度分布情况作一估算，把附图a所示的截片形状简化成为附图b所示的情形。已知T＝1700K，hg＝1000W（m2.K），T，＝400k，h＝250W/（m2.K）。试计算：（1）截面中最高温度及其位置；（2）单位长度通道上的热量。解：根据对称性选择1/4区域为计算区域，采用60x70网格，取壁面2＝15W（m·K）时得单位长度的传热量为987.8W，等温线分布如图所示。截面中最高温度发生在左上角，该处温度为1419.9C。综合分析与分析、论述题4-25、工业炉的炉墙以往常用红砖和耐火砖组成。由于该两种材料的导热了建虾线14/31口H田56，l令B/s187⊙C84％C□17：26P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.92Size:188.×传热学老师布置习题及……系数较大，散热损失较严重，为了节省能量，近年来国内广泛采用在耐火砖上贴一层硅酸纤维毡，如附图所示。今用以下的非稳态导热简化模型来评价黏贴硅酸纤维毡的收益：设炉墙原来处于与环境平衡的状态，＝0s时内壁表面突然上升到550℃并保持不变。这一非稳态导热过程一直进行到炉墙外表面的对流，辐射热损失与通过墙壁的导热量相等为止。在炉墙升温过程中外表面的总表面传热系数由两部分组成，即自然对流引起的部分2x）＝1.12（30-6y及辐射部分h，＝48o0T，Tm＝（T＋T，）/2其中：为外表面温度，1工，为内表面温度，6，＝240mm，62＝240mm，63＝40mm为简化计算，设三种材料的导热系数分别为么＝1.6W1（m.K），2＝0.8W/（m.K），＝0.04W/（m.K）。试计算每平方炉墙每平方面积上由于粘贴了硅酸纤维毡而在炉子升温过程中节省的能量。解：采用数值计算方法，详细过程从略。4-27、一家用烤箱处于稳定运行状态，箱内空气平均温度1＝155℃，气体与内壁间的表面传热系数h＝40W1（m2.K）。外壁面与20℃的周围环境间的表面传热系数h＝10W1（m2.K）。烤箱保温层厚30mm，2＝0.03W/（m.K），保温层两侧的护板用金属制成且很薄，分析中可不予考虑，然后，突然将烤箱调节器开大，风扇加速，内壁温功率控制器度突然上升到185℃，设升温过程中烤箱外壁面与环境间的表面传热系数可用h＝c-1，计算，环境温度＇仍保持为20℃，tw为烤箱外壁面温度，c之值与运行时一样。试确定烤箱内壁温度跃升后到达新的稳定状态所需时间。解：需采用数值方法求解，过程从略。5-8、已知：介质为25℃的空气、水及14号润滑油，外掠平板边界层的流动由层流转变为湍流的灵界雷诺数Re＝5×103，u。＝1m/s。求：以上三种介质达到Rec时所需的平板长度。15/31口H田56，l令B/s187⊙084％17:26P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.66Size:180.×传热学老师布置习题及……解：（1）25℃的空气v＝15.53×106m2/sRe，＝ux1×xV＝15.53×106＝5×103x＝7.765m（2）25℃的水v＝0.9055×106m2/sx＝0.45275m（3）14号润滑油v＝313.7×10-6m2/sx＝156.85m5-11、已知：如图，外掠平板的边界层的动量方程式为：ououo2u“ax＋ayy2求：沿y方向作积分（从y＝0到y≥6）导出边界层的动量积分方程。解：任一截面做y＝0到y→的积分根据边界层概念y＞，u≈uxu0.地在该处xay2u＝0y2（1）其中oy＂-ou由连续行方程可得00y＝-0oaysoudy，vs二s.oudyoaxudy＝-所以yaudy＋Jux。x（2）16/310H田56l令K0C84％□17：26P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:2.50Size:180.×传热学老师布置习题及……ou又因。y2y＝0.......（3）s.oudy-Lsoudy＋u-（1）（2）代入（3）ax”axy。s.ouoxdulu-u.dy故边界层的动量积分方程为-（）dxo5-12、已知：1.013×103Pa、100℃的空气以v＝100m/s的速度流过一块平板，平板温度为30℃。求：离开平板前缘3cm及6cm处边界层上的法向速度、流动边界层及热边界层厚度、局部切应力和局部表面传热系数、平均阻力系数和平均表面传热系数。100＋30＝65解：定性温度m22＝0.0293W/（m·K），Pr＝0.695，v＝19.5x106m21s，p＝1045kg/m3。Re，＝-＊-0.03×10010＝1.538×10（1）x＝3cm处，v19.5v＝100×0.87/（1.538×103）2＝0.2218m/5动量边界层厚度6＝4.64×0.03×（.538×10）2＝0.355mm6，＝Pr-36＝0.695-3×0.355＝0.398mm0.323pu20.323×1.045×1002Tw＝8.61kg/（m.s2）√Re，√1.538×105h，＝0.332～Rev2pr/3＝0.332x0.0293×√1.538×103×0.695＝112.6W/（m2.K）0.035-16、已知：将一块尺寸为0.2m×0.2m的薄平板平行地置于由风洞17/31H田56，l令K/s2.50C84％□17：26P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:0.94Size:188！×传热学老师布置习题及……造成的均匀气体流场中。在气流速度u。＝40m/s的情况下用测力仪测得，要使平板维持在气流中需对它施加0.075N的力。此时气流温度1。＝20℃，平板两平面的温度＝120℃。气体压力为1.013×103Pa。求：试据比拟理论确定平板两个表面的对流换热量。0.07512＝0.9375N/m2＝0.9375Pa解：0.2×0.2，边界层中空气定性温度为70℃，物性：p＝1.029kg/m3，cp＝1009J1（kg/K），v＝20.02×106m2/s，Pr＝0.694利用Chilton-Colburn比拟：j＝S1Pr213.＝1＝1X0.9375＝5.69×104，jn＝/3222pun/221.029×402/22puoCph＝pu.CpPr2/3＝5.69×10×1.029×40×1009x0.694-/3＝23.6x1.276＝30.1W/（m2·K）＝2hA（t-t）＝2x3.01×0.22×（120-20）＝240.9W这说明Chilton--Colburn比拟对层流运动也是适用的，即适用于平均值也适用于局部值。6一1、在一台缩小成为实物1/8的模型中，用20℃C的空气来模拟实物中平均温度为200℃空气的加热过程。实物中空气的平均流速为6.03/s，问模型中的流速应为若干？若模型中的平均表面传热系数为195W1（m2K），求相应实物中的值。在这一实物中，模型与实物中流体的P数并不严格相等，你认为这样的模化试验有无实用价值？18/31口2.5H田56l令K/s0C84％□17：26P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:0.94Size:179.×传热学老师布置习题及……解：根据相似理论，模型与实物中的Re应相等空气在20C和200C时的物性参数为：20C:v1＝15.06×10-6m2/s，＝2.59×102W/m·K，Pr＝0.703200C:v，＝34.85×106m2/s，，＝3.93×10-2W/m·K，Pr，＝0.680多VIV2→u＝（）e）u15.06×8×6.03＝20.85m/sV2434.85又Nu，Nu，得：h2＝h（-（）＝195x3.93＝36.99W1（m2.K）1282.59上述模化试验，虽然模型与流体的P数并不严格相等，但十分相近这样的模化试验是有实用价值的。6一2、对于恒壁温边界条件的自然对流，试用量纲分析方法导出：Nu＝f（Gr，Pr）。提示：在自然对流换热中ga△起相当于强制对流中流速的作用。解：h（ga△t）017＜［mer-］［Lr-］［meLr-］［ML］［z20-T-2］［ML＇T-］［L］n-r＝7-4＝3→（n，π2，π3）＝0则各准内涵表达式如下n，＝hL＂2n＂（ga△r）2＝pL2a2n2（ga△t）d23＝cL33n3（ga△t）3展开：1＝M0T3LMb10bT--cLT-21＝M1＋b1＋c1g-1-61T-3-361-1-2d101＋61-1＋d1解得：b1＝-1，cl＝0，d1＝0，al＝119/313.2H田56l令K/s0C84％□117：26P:0/1dX:7.5dY:-6.4Xv:0.381Yv:-0.324Prs:0.98Size:179.×传热学老师布置习题及……n1＝hL＇x＇n°（ga△）°＝hL/a＝NuT2＝ML-L2M520-02LD2T-362M2L-2T-2L42T-202＝M1＋b2＋C21-3＋02＋62-C2＋2-62T-32-C2-12→b2＝0，c2＝-1，d2＝1/2，a2＝3/2各系数乘以2得：2＝p2L2n-2（ga△t）＇＝°gatL3/v3＝Gr3＝L20-T-2L3Mb30-b3L53T-3b3M3Lc3T-c3L3T243＝L2＋a3＋b3-c3＋d301-b3T-2-3b3-c3-3d3Mb3＋c3→b3＝-1，c3＝1，d3＝0，a3＝0丌3＝cL＂x＇n＇（ga△1）°＝cn/a＝Pr即原则性准则方程：Nu＝f（Gr，Pr）6一12、已知：一直管内径为2.5cm、长15m，水的质量流量为0.5kg/s，入口水温为10℃，管子除了入口处很短的一段距离外，其余部分每个截面上的壁温都比当地平均水温高15℃。求：水的出口温度。并判断此时的热边界条件。解：假使出口水温1＝50℃，则定性温度11-（＋）＝50＋30＝302℃，水的物性参数为2＝0.618W/（m·K），7＝801.5×106kg/（m·s），Pr＝5.42，4m4×0.5×106Re＝31771＞104ndu3.1416×0.025x801.5。因＇w-1＝15℃，不考虑温差修正，则N“g＝0.023×317718×5.424＝180.7Nu2180.7×0.61h＝＝4466.9W/（m2.K）0.025中1＝hdl（t-t，）＝4466.9×3.1416×0.025×15×15＝78.94kW另一方面，由水的进口焓i＝42.04kJ1kg，出口i＝209.3kJ/kg，得热量20/315H田56l令K0C84％□17：26P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.49Size:171.×传热学老师布置习题及……2＝m（i-i）＝0.5×（209.3-42.04）＝83.67kW2＞中1，需重新假设，直到1与2相符合为止（在允许误差范围内）。经过计算得1＝47.5℃，1＝中2＝78.4kW。这是均匀热流的边界条件。6一14、已知：1.013×103Pa下的空气在内径为76mm的直管内流动，入口温度为65℃，入口体积流量为0.022m31s，管壁的平均温度为180℃。求：管子多长才能使空气加热到115℃。65＋115＝90解：定性温度2一℃，相应的物性值为：p＝0.972kg/m3cp＝1.009kJ/（kg·K），＝3.13×102W/（m·K），u＝21.5×106kg/（m·s），PF＝0.690在入口温度下，P＝1.0045kg/m3，故进口质量流量：i＝0.022m3/sx1.0045kg/m3＝2.298×10-2kg/s，4m4×2.298×102×106Re＝＝17906＞10mdu3.1416×0.076×21.5，先按l1d＞60计，Nuo＝0.023×1790608×0.6904＝50.08，h＝50.08×0.0313＝20.62W/（m2.K）0.076空气在115℃时，cp＝1.009kJ（kg·K），65℃时，cp＝1.007kJ1（kg·K）。故加热空气所需热量为：中＝m（Cn-c）＝0.02298×（1.009×103×115-1.007×103×65）＝1162.3W采用教材P165上所给的大温差修正关系式：三273＋900.53363）053273＋180453＝0.885所需管长：中1162.31＝2.96mndh（t-ty）3.1416×0.076×20.62×0.885×（180＝90）21/31H田56令K/s3.30C84％□17：26P:0/1dX:-2.9dY:0.5Xv:-0.101Yv:0.013Prs:0.88Size:179.×传热学老师布置习题及……11d＝2.96/0.076＝38.6＜60，需进行短管修正。采用式（5-64）的关系式：cy＝1＋（d/1）＝1.0775，所需管长为2.96/1.0775＝2.75m。6-25、已知：冷空气温度为0℃，以6m/s的流速平行的吹过一太阳能集热器的表面。该表面尺寸为1m×1m，其中一个边与来流方向垂直。表面平均温度为20℃。求：由于对流散热而散失的热量。0＋20解：1y＝2＝10℃10℃空气的物性y＝14.16×106，＝2.51×102，PF＝0.705ul_6x1.0y14.16×106＝4.23728×103Re，11Nu＝0.664Re2Pr3＝384.68h＝384.68×2.51×102＝9.655w/（m2.k）1.0s＝1x1＝1.0m2＝h·s（t-1o）＝9.655×（20-0）＝193.1w6-34、已知：可以把人看成是高1.75m、直径为0.35m的圆柱体。表面温度为31℃，一个马拉松运动员在2.5h内跑完全程（41842.8m），空气是静止的，温度为15℃。不计柱体两端面的散热，不计出汗散失的部分。求：此运动员跑完全程后的散热量。41842.84＝4.649m/s31＋15＝23解：平均速度“2.5×3600，定性温度”2℃，空气的物性为：＝0.0261W/（m·K），v＝15.34×106m2/s，Pr＝0.702，4.649×0.35Re15.34×16＝106072＞4×10，按表5-5.有：22/314.4条H田56l令K/s◎0C84％□17：26P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:4.01Size:188.×传热学老师布置习题及……Nu＝0.0266Re0805＝0.0266×106072.805＝295.5，h＝295.5x0.0261/0.35＝22W/（m2.K）＝Ah△t＝3.1416×0.35×1.75×22×（31-15）＝677.3W在两个半小时内共散热2.5×3600×677.3＝6095960＝6.096×10°J6-38、已知：在锅炉的空气预热器中，空气横向掠过一组叉排管束，s1＝80mm，s2＝50mm，管子外径d＝40mm，空气在最小界面处的流速为6m/s，tw＝133℃，在流动方向上排数大于10，管壁平均温度为165℃。求：空气与管束间的平均表面传热系数。t＋1_133＋165＝149解：定性温度t＇＝tm＝22℃，得空气物性值为：＝0.0356W1（m·K），v＝28.8×106m2/s，Pr＝0.683，Re＝ud6x0.04＝8333，由＝2，2＝1.25V28.8×106dd据表（5-7）得C＝0.519，m＝0.556，∴Nu＝0.519×83330556＝78.55h＝Nua_78.55x0.035669.9w（m2.K）d0.046-43、已知：假设把人体简化为直径为30mm、高1.75m的等温竖柱体，其表面温度比人体体内的正常温度低2℃。不计柱体两端面的散热，人体温度37℃，环境温度25℃。求：该模型位于静止空气中时的自然对流换热量，并与人体每天的平均摄入热量（5440kJ）相比较。1m35＋25＝30解2℃＝0.0267W/（m·K），v＝16×10-6m2/s，Pr＝0.70123/31口4.4H田56l令K/s0C84％□17：26P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:2.84Size:171.×传热学老师布置习题及……110＝30＋270303＝98xx（35-25）Gr＝8a△1.753＝6.771×109303（16×10-6）月处于过渡区。Nu＝0.0292×（6.771×109×0.701）039＝0.0292×（4.746×10）03％＝173.4hNu2_173.4×0.0276＝2.646W（m2K）d1.75＝Ah△t＝3.14×0.3x1.75×2.646×（35-25）＝43.62W一昼夜散热Q＝43.62×24×3600＝3769kJ。此值与每天的平均摄入热量接近，实际上由于人体穿了衣服，自然对流散热量要小于此值。7-6、饱和温度为50℃的纯净水蒸汽在外径为25.4mm的竖直管束外凝结，蒸汽与管壁的温差为11℃，每根管于长1.5m，共50根管子。试计算该冷凝器管束的热负荷。50＋（50-11）＝44.5解：2C，P＝990.3kg＝0.641/（mk），＝6065×10＊，r＝2382.7×10人g，设流动为层流，1.13h＝Lu，L（t-t）1.13982383×1099032×06417L606.5×10-6×1.5×11＝49548m）4hLt4×4954.8×1.5×11R，＝m，2.383×10°×606.5×10＝226.3＜1600，故为层流。整个冷凝器的热负荷Q＝50×4954.8×3.1416×0.0254×1.5×11＝326.2kW。7-13、一卧式水蒸汽冷凝器管子的直径为20mm，第一排管子的壁温1w＝15℃，冷凝压力为4.5x103Pa。试计算第一排管子每米长的凝结液量。解：相应于4.5×103Pa的饱和温度为30.94℃，，1-3094＋15＝22972321℃。P1＝997.5kg/m3，＝0.605W1（m.K），u1＝943.3x10kg/（ms），r＝2438.5×103J/kg，△t＝30.94-15＝15.94℃，24/31HD56l令3.9K/s⊙084％117:26P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:4.32Size:188.×传热学老师布置习题及……0.7259.8×2438.5×103×997.52×0.60537＝8340W/（m2k）h＝943.3×10-6×0.02×15.94每米长管子上的凝结水量：G＝mdhA1_3.1416×0.02×8340x15.94＝3.425×10-3kg/s＝12.33kg/hr2438.5×107-20、平均压力为1.98×10Pa的水，在内径为15mm的铜管内作充分发展的单相强制对流换热。水的平均温度为100℃，壁温比水温高5℃。试问：当流速多大时，对流换热的热流密度与同压力、同温差下的饱和水在铜表面下作大容器核态沸腾时的热流密度相等？解：P，＝1.98×102Pa时，t，＝120℃，对应水的物性D＝0.252x106m2/s，P，＝1.47，＝0.686W/（m·K）根据公式h＝C，4233p05＝0.1224×5233×（1.98×103）05＝2315.87W/（m2·K）由题意，要使二者热流密度相等，在温差相同情况下，必须表面传热系数h相等。对管内湍流强制对流h＝0.023Rp，a而h＝h＇R08hd2315.87×0.015所以”0.023P40.023×1.4704×0.686＝1887.24R，＝12439R-udR，_12439×0.252×106＝0.21m/s而ev所以d0.0157-24、一台电热锅妒，用功率为8kw的电热器来产生压力为1.43X103Pa的饱和水蒸汽。电热丝置于两根长为1.85m、外径为15mm的钢管内（经机械抛光后的不锈钢管），而该两根钢管置于水内。设所加入的电功率均用来产生蒸汽，试计算不锈钢管壁面温度的最高值。钢管壁厚1.5mm，导热系数为10w/（m·K）。8000解：由已知条件可得，热流密度9＝2x3.1416x1.85×0.015＝45882W/m2在1.43×105Pa压力下：P1＝951kg/m3，P，＝0.8265kg/m3，cp＝4233J1（kg·K），r＝2691.3x103J/kg，y＝569×104N/m，17，＝259×106kg/（m·s），2＝0.685W/（m·K），Pr，＝1.60代入式（6-17）有：0.331＝2691.3x103x1.6045882569×10-4×0.0132×4233259×10-6×2691.3×103V9.8×（951-0.8265）25/31HD56l令15.1K/s⊙084％□117：26P:0/1dX:1.9dY:3.5Xv:0.104Yv:0.224Prs:2.90Size:179×传热学老师布置习题及……△t＝7.37℃，∴1＝120＋7.37＝127.4℃。不锈钢管内的热量都是通过内壁面导出的，导热温差：△t＝ln（d2/d1）/（2元1）＝4000In（15/12）/（2x3.1416x10x1.85）＝7.68℃。最高壁温位于内壁面上，其值为127.4＋7.68＝135.1℃。8-8、试确定一个电功率为100W的电灯泡发光效率。假设该灯泡的钨丝可看成是2900K的黑体，其几何形状为2mm×5mm的矩形薄片。E，2解：100可见光的波长范围0.38～0.76m则T＝1102m.K；22T＝2204um.K由表可近似取F（0-038）＝0.092；Fb（0-0.76）＝10.19AE＝CT在可见光范围内的能量为100×（10.19-0.094）％7△E＝10.09％发光效率E8-9、钢制工件在炉内加热时，随着工件温度的升高，其颜色会逐渐由暗红变成白亮。假设钢件表面可以看成黑体，试计算在工件温度为900℃及1100℃时，工件所发出的辐射能中的可见光是温度为700℃的多少倍？T≤600um.K时Fb0-）＝0:T＝800um.K时Fb（o-）＝0.16x10解：解：（1）t＝700C时，T＝973K，T＝0.38×973＝369.7，umK，Fb（0-）＝0.00T＝0.76x973＝739.5wmK，由AT≤600umK及T＝800umK之F0-）值线性插值得：Fb0-4）＝1.116×103，Fb（-4）＝1.116×10-5＝0.001116％可见光的能量为：1.116×10×5.67×9.73＝0.5672W/m2.（2）1＝900℃时，T＝1173K，T＝0.38×1173＝445.7umK，F0-4）＝0.002T＝0.76×1173＝891.5mK，F0-4）＝1.565x10，F）＝1.565×10＝0.01565％，此时可见光的能量1.565×10×5.67×11.73＊＝16.8W/m2所以900℃时是700℃时的16.3/0.5672＝29.6倍.（3）1＝1100C时，T＝1373K，么T＝0.38×1373＝521.74umK，F0-4）＝0.00元2T＝0.76×1373＝1043.48umK，Fb（-）＝5.808×10，F（4-）＝5.808×104＝0.05808％，此时可见光的能量为5.808×10-4×5.67×13.734＝117.03W/m2所以1100℃时是700℃时的117.03/0.5672＝206.3倍.8-11、把地球作为黑体表面，把太阳看成是T＝5800℃的黑体，试估算地球表面温度。已知地球直径为1.29×10m，太阳直径为1.39×10m，两者相距1.5×10＂m。地球对太空的辐射可视为0K黑体空间的辐射。26/31口5。川K1s10.4⊙0C84％□17：26P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.39Size:188.×传热学老师布置习题及……解：如图所示。地球投影面积对太阳球心的张角为：5800k1.60×10＇△S2＝/4×（1.29×10）0.785×1.6641×104＝0.5806×10-8（1.5×10＂月2.25×1022（球面角）△Q0.5806×10-8＝4.6226×10-1044×3.14。地球表面的空间辐射热平衡为：中5c＝4R2m×0，×4.623×10-10A，Eb-s.c＝0，A，＝4R2＝4x3.14x.29×1022Ee＝o，T4，o，T4×4x3.14×29×1072＝4RmXo，Tm4×4.623×10-10（.29×107）T，＝（1.39×109）Tmm6×4.623×10-10T＝Tm×1.392×108×4.623×10-10×10-4/1.292］VA＝5800×1.9321×4.623/1.6641×10-6］4＝5800×（5.3675×10-6）＝5800×1.5221/31.62＝279.2K8-24、一测定物体表面辐射特性的装置示于附图中。空腔内维持在均匀温度T，＝1000K；腔壁是漫灰体＝0.8。腔内1000K的热空气与试样表面间的对流换热表面传热系数h＝10W/m2.K。试样的表面温度用冷却水维持，恒为300℃，试样表面的光谱反射比示于附图。试：（1）计算试样的吸收比；（2）确定其发射率；（3）计算冷却水带走的热量。试样表面A＝5cm2。解：冷却水带走的热量为：＝com＋od，中cn＝5×10×10×（1000-600）＝5×10-×10×400＝2W，a＝0.8End2＋0.2E，xdaE-F＝0864000）EadaE＝1-Fb（0-1）＝1-0.8564＝0.1436，a＝1-P2∴md＝（0.8×0.8564＋0.2×0.1436）×E，×A27/31H56，l令5.3K/s0C84％□17：26P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.44Size:204.×传热学老师布置习题及……＝5×10-1×5.67×10-8×10004×0.7138＝5×104×5.67×100.7138＝20.23W，中＝中cn＋中md＝2＋20.23＝22.23W，吸收比＝0.7138，反射比＝0.2862.反射率应以600K来计算。（1-0.2）E2d2（1-0.8）Eda14.056＝X2400K0.8＋0.2×14.05E，E100100＝0.8×0.1405＋0.2×0.8595＝0.1124＋0.1719＝0.3967所以＝22.23W，发射率￡＝0.397，吸收比a＝0.714。9-6、试用简捷方法确定本题附图中的角系数X1.2°解：（1）因为X2＝1X12＝A2-2RA12πRx3/4＝0.4244（2）因为X2.＝1（a）在垂直于纸国方向无限长（b）半球内面与底面X12A2_TR2A2πR2＝0.5（3）参考（2），具有对称性，X12＝0.5/4＝0.125（4）假设在球得顶面有另一块（c）半球内表面与1小4底面（d）球与无限大平面无限大平板存在，由对称性知X12＝0.59-20、已知：一有涂层的长工件表面采用如图所示方法予以加热烘干，加热器表面T，＝800K，＆T＝1，工件表面Tp＝500K，Ep＝1。工件及加热表面在垂直于纸面方向均为无限长。b＝0.15m，bp＝0.3m，1＝0.2m。对流不考虑，工件的另一面绝热。（1）环境为300K的大空间；（2）环境是绝热的。求：上面两种情形下施加在单位长度加热器上的电功率。解：如图所示：28/31四56llK/084％117：26P:1/1X:841.9Y:13.5Xv:0.0Yv:0.0Prs:1.71Size:147.×传热学老师布置习题及……0.1520.21360.21361/0.20.3Eor1/.p8003.Jwum（1）环境为300K的黑体，则单位长度的加热表面的辐射换热量为：④1＝A.［X.（T.-T）＋x.（T-T＂），利用交叉线法：X，.p＝301×2-0.2136×2-0.602-0.4272＝05827X.＝1-X.＝04173，2×0.150.3中L＝5.67×10×0.15×［0.583×（800＊-500）＋0.417×（800-300＊）］＝5.67×0.15×［0.583×（4096-625）＋0.417×（4096-81）］＝0.8505×［2023.6＋1674.3］＝0.8505×3697.9＝3145W/m（2）设环境为重复辐射表面，则：Xp＝0.583，Xs＝0.417＝X，.pApA＝0.5830.15＝0.2920.3Xp＝1-Xp＝1-0.292＝0.708①L1Es-Ep111因此有：RagR.pR，，＋R.s，11R.＝AX.0.15×0.58311.435m11＝15.987m1R＝A，X0.15x0.41711R＝A，X0.3x0.7084.708m129/310。合k/s0C84％□17：26P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.58Size:180.×传热学老师布置习题及……11Rg＝1/R.R＋R1/11.435＋1/（15.987＋4.708）0.08745＋0.048321＝7.365m-0.135775.67×108×（8004-500）5.67×（4096-625）①L一＝2672W/m7.3657.3659-25、已知：上题中取＝62＝0.8，3＝0.025，T与T2一定。求：加入遮热板后1、2两表面间的辐射换热减少到原来的多少分之一。解：无遮热板时，q1.2＝（E-E2），加入遮热板后，q13＝6（E1-Es），93.2＝62（E3-E2），达到稳态时，913＝q93.2＝92，＝（＋9sa）＝，（En-Es）＋6，（Es-E.）］-2a（En-Ea）.6140-1.-108100-1）/8108-111/11.5012×40.2571.5080.5053.79-32、已知：如上题，在吸热表面上加了一层厚8cm的空气夹层（空气压力为1.013×10Pa），夹层顶盖玻璃内表面的平均温度为40℃，玻璃穿透比为0.85，其他条件不变。求：此情形下集热器的效率。解：9吸＝800×0.85×0.9＝612W/m2，中吸＝1.2×612＝740.5W；辐射散热量：（磊）-（）门5.67×1.21×（3.63-3.13）＝105.2W1/81＋1/82-11/0.2＋1/0.94-190＋40定性温度”2＝65℃，无＝0.0293，v＝19.5×106，P＝0.695，9.8×0.083×（90-40）Grs（273＋65）×19.52×102＝1.952x10°，30/315。川s◎084％117：26P:1/1X:795.5Y:7.0Xv:0.0Yv:0.0Prs:1.40Size:130.×传热学老师布置习题及……GT·PF＝1.952×10°×0.695＝1.357×10°据式（5-90），Nu＝0.061×（1.357×10°）＝6.753h＝甲散＝中。＋，＝105.2＋1.21×2.473×50＝254.8W-中服×100％＝740.5-254.6100％＝65.6％740.531/31口H田56ll令K/s0⊙084％117：28P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.16Size:188×传热学习题集和答案详……目录第1章“绪论”习题解答…1第2章“导热问题的数学描述”习题解答………6第3章“稳态导热”习题解答……16第4章“非稳态导热”习题解答……….35第5章“导热问题数值解法”习题解答…….…….54第6章“对流换热的基本方程”习题解答………67第7章“对流换热的求解方法”习题解答…………71第8章“单相流体对流换热及其实验关联式”习题解答……93第9章“凝结换热与沸腾换热”习题解答……133第10章“热辐射的基本定律”习题解答……149第11章“辐射换热计算”习题解答…………159第12章“传热和换热器”习题解答……………192附录………218附录1重庆大学2005年硕士研究生传热学入学考试试题及答案……218附录2重庆大学2006年硕士研究生传热学入学考试试题及答案.……224附录3重庆大学2007年硕士研究生传热学入学考试试题及答案……230附录4重庆大学2008年硕士研究生传热学入学考试试题及答案….2372/245口H四56，l令124K/s84％□117：28P:1/1X:752.7Y:17.7Xv:0.0YV:0.0Prs:1.63Size:139.×传热学习题集和答案详……第1章“绪论”习题解答夏展；虫起，中1.热量、热流量与热流密度有何联系与区别？【答】热量Q，其单位为J（kJ）；本教材中热流量记作，其单位为W（kW），是单位时间内传递的热量，又称传热速率；热流密度q，其单位为W/m2（kW/m2），9是单位时间内通过单位面积所传递的热量。如记为传热时间，则三者间有如下的关系：精Q＝T＝qAT式中，A为传热面积，m2。单血离如取火3试2.“热对流”与“对流换热”是否为同一现象？试以实例说明。对流换热是否属于基本的传热方式？【答】热对流与对流换热是两个不同的概念，属于不同现象。其区别为：①热对流是传热的三种基本方式之一，而对流换热不是传热的基本方式；②对流换热是导热和热对流这两种基本传热方式的综合作用，由于流体质点间的紧密接触，热对流也同时伴随有导热现象；③对流换热必然具有流体与固体壁面间的相对运动。工程中流体与温度不同的固体壁面因相对运动而发生的传热过程称为对流换热。变＋3.用水壶将盛装的开水放在地面上慢慢冷却，开水以哪些方式散发热量？打开水壶盖和盖上水壶盖，开水的冷却速度有何区别？，【答】水壶与地面间以导热方式传递热量；水壶与周围空气间以自然对流换热方式传递热量，与周围环境以辐射换热方式传递热量；壶嘴以蒸发方式散发热量。打开壶盖后，开水的蒸发速度加快，开水因此冷却得更快。wOf4.夏季在维持20℃的空调教室内听课，穿单衣感觉很舒适，而冬季在同样温度的同一教室内听课却必须穿绒衣。假设湿度不是影响的因素，试从传热的观点分析这种反常的“舒适温度”现象。【答】夏季人体的散热量为：01一Y3/245口H56，l令112K/s084％□117：28P:1/1X:782.5Y:0.0Xv:0.0Yv:0.0Prs:1.0Size:114.×传热学习题集和答案详…第1章“绪论”习题解答因①＝h（t2-t）A204故＝0-A＝（-5972℃＝-11.48℃10×5×39.上题中，如果采用膨胀珍珠岩配置轻质混凝土浇铸制成的墙板［入＝0.1W/（m·℃）］代替黏土砖墙，设两者厚度相等，室内外表面温度保持不变，热损失减少了多少？【解】＇入（tM-t2）A＝0.10.25×（15＋5）×5X3W＝120W△①＝-＝（972-120）W＝852W减少百分比为：Ped部可△中852中972×100％＝87.7％10.炉子的炉墙厚13cm，总面积为20m2，平均导热系数为1.04W/（m·℃），内外壁温分别为520℃和50℃。试计算通过炉墙的热损失。如果燃煤的发热值为2.09×104kJ/kg，问每天因热损失要多用掉多少煤？【解】中（t1-t2）A＝1.04×（520-50）×20W0.13＝75200WM＝24×360024×3600×7.52×104kg＝310.9kg902.09×101DtO0＝8:1即每天因热损失要多用掉煤310kg。11.竖直管道高20m，管内径为15mm，进口温度为25℃的冷水经管道后被加热到40℃，冷水的质量流量为0.25kg/，水的比定压热容为4.174kJ/（kg·℃）。试求：①水的加热量为多少？②若考虑位能，水的总能量增大多少？③设管内壁温度为55℃，水的平均温度取进出口平均值，求表面传热系数。【解】①p＝Mc，（t2-tn）＝0.25×4.174×（4025）kWmH2，R8＝15.6525kW1）X＋8.1②△＝Mg△z＝0.25×9.81×20W＝49.05W—35/245HD56，l令112K/s084％□117：28P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.78Size:163×传热学习题集和答案详……第1章“绪论”习题解答因①＝h（t2-t）A20故更＝0-A＝（-5972℃＝-11.48℃10×5×39.上题中，如果采用膨胀珍珠岩配置轻质混凝土浇铸制成的墙板［入＝0.1W/（m·℃）］代替黏土砖墙，设两者厚度相等，室内外表面温度保持不变，热损失减少了多少？【解】＇入（tm-t2）A＝0.10.25×（15＋5）×5×3W＝120W△①＝①-′＝（972-120）W＝852W减少百分比为：△中_852中972×100％＝87.7％10.炉子的炉墙厚13cm，总面积为20m2，平均导热系数为1.04W/（m·℃），内外壁温分别为520℃和50℃。试计算通过炉墙的热损失。如果燃煤的发热值为2.09×104kJ/kg，问每天因热损失要多用掉多少煤？【解】中（t1-t2）A1.04×（520-50）×20W70.13＝75200WM＝24×3600中24×3600×7.52×104kg＝310.9kg9o2.09×10足代，00＝：即每天因热损失要多用掉煤310kg。11.竖直管道高20m，管内径为15mm，进口温度为25℃的冷水经管道后被加热到40℃，冷水的质量流量为0.25kg/s，水的比定压热容为4.174kJ/（kg·℃）。试求：①水的加热量为多少？②若考虑位能，水的总能量增大多少？③设管内壁温度为55℃，水的平均温度取进出口平均值，求表面传热系数。【解】①p＝Mc，（t2-tn）＝0.25×4.174×（40-25）kWmH2，R8＝15.6525kW）x＋E.1（-n）＝g②△＝Mg△z＝0.25×9.81x20W＝49.05W—35/245HD56l令270B/sC84％□17：28P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.66Size:188！×传热学习题集和答案详……传热学习题解答＝＋中冬季人体的散热量为：式中：中，分别为夏季和冬季人体的总散热量；中，中分别为夏季人体的对流换热量与辐射换热量；，分别为冬季人体的对流换热量与辐射换热量。己密团单由于冬夏两季室内的风速变化不大，因此对流换热量y～Φv；但由于人体与围护结构内壁面的温差冬季远大于夏季，辐射换热量＞更，所以在室温相同时，中＞中，说明人体冬季散热量更多，为维持热舒适，冬季应多穿或者穿厚一些的衣物。民妆量5.用厚度为δ的2块薄玻璃组成的具有空气夹层的双层玻璃窗和用厚度为26的1块厚玻璃组成的单层玻璃窗传热效果有何差别？试分析存在差别的原因。一同火否星吉【答】双层玻璃窗增加了空气夹层，通常夹层厚度δ远小于窗的高度，自然对流难以展开，且空气的导热系数很小，因此增加了空气层热阻，传热系数比单层玻璃窗更小，保温效果更好。派①：限合6.略。本基两购早剪清快氏才:7.图1.3中（见教材P4），壁内的温度变化用连接tm和t2的直线表示，即壁内温度分布呈线性规律。若t和t保持不变，什么情况下温度分布呈非线性？身阳主发面医恢的固面不面防国不更盖【答】当壁内具有内热源或者壁体材料导热系数随温度发生变化时，壁内温度分布为非线性分布。本盖明盖壶本？量国8.长5m，高3m，厚250mm的普通黏土砖墙，在冬季供暖的情况下，如果室内外表面温度分别为15℃和-5℃，黏土砖的导热系数为0.81W/（m·℃），试求：通过该砖墙的热损失；如已知墙外壁与大气间的表面传热系数为10W/（m2.℃），求大气温度。更费因【解】由于室温高于室外气温，热量由室内传递到室外，墙体以导热方式传递的热量为：彩内室薄一国夏盛料国李中＝入0.81（twl-t2）A＝0.25（15＋5）×5×3W＝972W一2-4/245H田56l令B/s2890C84％□117：28P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:4.32Size:188×传热学习题集和答案详……别传热学习题解答上△49.05×100％＝0.31％中-15652.5可见，考虑位能后总能量仅增加了0.31％，完全可以忽略不计。t1＝2（tn＋to）＝32.5℃③因更＝h（t-t）Tdl，故15652.5hW/（m2.℃）w0（tw-t）Tdl7（55-32.5）×3.14×0.015×20＝738.5W/（m2·℃）12.在一次测定空气横向外掠单根圆管的对流换热实验中，得到下列数据：管壁平均温度t＝69℃，空气加热前后平均温度t＝20℃，管子外径d＝14mm，加热段长80mm，输入加热段的功率为8.5W。如果全部热量通过对流换热传给空气，求此时的对流换热表面传热系数。盛内（0·）N7/-0【解】更＝h（t-t）Tdlh＝（t-t）mdl8.5（69-20）×3.14×0.014×0.08W/（m2.℃）＝49.3W/（m2.℃）00513.求传热过程的总热阻、传热系数、散热量和内外表面温度。已知：8＝360mm，室外温度t2＝-10℃，室内温度t＝18℃，墙的导热系数入＝0.61W/（m·K），内壁表面传热系数h1＝8.7W/（m2·K），外壁传热系数h2＝24.5W/（m2·K）。11-110.36，141e【解】Rh＋h，（8.7＋0.61＋24.5）m2·℃/W容盛平0.746m2。℃/W内好大总的本，k＝1装面美，平口由＝1.34W/（m2·℃））ll＝①【）q＝k（tn-t）＝1.34×（18＋10）W/m2＝37.5W/m2因q＝h1（tn-tmi）＝h2（t2-t）ex20＝g＝4-6/245H田56l令K/s1320C84％□117：28P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.33Size:171.×传热学习题集和答案详……第1章“绪论”习题解答故tl＝tn＝（18-37.5h8.7℃＝13.68℃答＝n＋-（10＋℃章美＝-8.47℃14.两平行大平壁A和B构成一空气夹层。平壁A厚12mm，壁体材料的导热系数为1.2W/（m·K），外表面温度为42℃，内表面温度为40℃；平壁B内表面温度为17℃，两壁面表面间的系统辐射系数C1.2＝3.96。求两壁内表面间的辐射换热量和夹层内空气与壁面间的自然对流换热量。【解】热量以导热方式从大平壁A的外表面传递到内表面，在稳态传热过程中，这部分热量以辐射换热的方式和对流换热的方式通过空气夹层传递到大平壁的内表面，空气夹层内的传热属于复合换热过程。:余的量买9＝入（tm-t2）1.2比更20.012（42-40）W/m＝200W/m2直亚新等公书面音氏新诉量9＝I（）-（门长3.96×（95.98-70.73）W/m2＝100W/m29e＝q-qr＝（200-100）W/m1＝100W/m215.一玻璃窗，尺寸为600mm×300mm，厚为4mm。冬天，室内及室外温度分别为20℃和-20℃，内表面的自然对流表面传热系数为10W/（m㎡·℃），外表面的强迫对流表面传热系数为50W/（m2·℃），玻璃的导热系数为0.78W/（m·℃）。试求通过玻璃窗的热损失。【答】中＝59.76W/m2景壳长司用家—5—7/245口H田56l令K1s288⊙0C84％□117：28P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.23Size:179.×传热学习题集和答案详……第2章“导热问题的数学描述”习题解答望1.试写出傅里叶定律的一般形式，并说明其中各个符号的意义。【答】q＝-入gradt。式中：gradt是空间某点的温度梯度，q为梯度方向上的热流密度，入是物体的导热系数，式中“-”表明热流总是与温度梯度方向相反。2.已知导热物体中某点在x，y，z三个方向上的热流密度分别为92，9，92，如何获得该点的热流密度矢量？【答】矢量大小：9＝9＋9＋q2，我特矢量的方向余弦：yycosB93.不同温度的等温面（线）不能相交，热流线能相交吗？热流线为什么与等温线垂直？【答】热流线也不能相交，这是因为与热流线垂直方向没有热流分量。如热流线不垂直于等温线，则等温线上必有一热流分量。而等温线上无温差，9＝0，只有热流线垂直于等温线才能使等温线上的分热流为零。4.根据对导热系数主要影响因素的分析，试说明在选择和安装保温隔热材料时要注意哪些问题。【答】①根据工作温度选择适合的保温材料；②进行保温计算时应考虑温度对保温材料导热系数的影响；③选择导热系数小的材料，其密度在最佳密度附近，使其具有最佳保温性能；④保温材料的保温性能受水分影响很大，必须采取防水措施；⑤采用各向异性材料时要注意导热方向对导热系数的影响。5.冰箱长期使用后外壳上易结露，这表明其隔热材料性能下降。—6一8/245HD56l令288K/s084％□117：28P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.0Size:179.传热学习题集和答案详……第2章“导热问题的数学描述”习题解答你知道其道理吗？（提示：冰箱隔热材料用氟利昂发泡，长期使用后氟利昂会逸出，代之以空气）【答】冰箱隔热材料为用氟利昂作发泡剂的聚氨脂泡沫塑料，其导热系数要比一般保温材料小。由于孔中氟利昂气体导热系数较低，随着使用时间的延长，气孔中氟利昂逐步逸出，环境中的空气取而代之。由于空气的导热系数是氟利昂的2～3倍，进入空气的隔热材料导热系数增大，致使冰箱保冷性能下降。6.导热系数入和热扩散率a有何区别？【答】导热系数入和热扩散率a是两个不同的物理量。前者仅指材料导热能力的大小，而后者综合了材料的导热能力和单位体积的热容量大小。导热系数小的材料热扩散率不一定小。如气体的导热系数很小，可是其热扩散率a却和金属相当。7.得出导热微分方程所依据的是什么基本定律？70081081【答】傅里叶定律和能量守恒定律。面两塑甲①8.试分别说明导热问题3种类型的边界条件。【答】第一类边界条件：已知任意时刻物体边界上的温度分布；第二类边界条件：已知任意时刻物体边界上的热流密度或温度梯度；第三类边界条件：已知任意时刻物体边界与周围流体间的对流换热情况，即已知表面传热系数h和周围流体温度tro如面9.对于第一类边界条件的稳态导热问题，其温度分布与导热系数有没有关系？【答】导热问题的完整数学描述包括导热微分方程和定解条件。在导热系数为常数的稳态导热问题中，只有第一类边界条件下的无内热源稳态导热问题的分析解才与导热系数没有关系，即导热系数只影响热流量，而不影响温度场。10.一维无限大平壁的导热问题，两侧给定的均为第二类边界条件，能否求出其温度分布？为什么？【答】不能求出。因为第二类边界条件所对应的是温度曲线的斜率，与绝对温度没有对应关系。11.有人对二维矩形物体中的稳态、无内热源、常物性的导热问题19/245H田56l令K/s1060C84％□117：28P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.46Size:204.×传热学习题集和答案详……养预传热学习题解答章进行了数值计算。矩形的一个边绝热，其余三个边均与温度为的流体发生对流换热，这样能预测温度场的解吗？其【答】根据所给边界条件，可以判断该物体没有热流，所以物体各点温度均为toL吊外12.在青藏铁路建设中，采用碎石路基可有效防止冻土区的冻胀和融降间题，为什么？，浴一￡阳料展【答】碎石路基中的空隙可以有效阻止热量自上而下的传递，而能顺利地将冻土层的热量自下而上的传递。其原因是：空隙内的空气的自然对流能将下方的热量传递到上方，而不能将上方的热量传递给下方，即路基中热量只能单向传递，这样就可以维持路基下冻土层的常年冻结。一政小一不黄13.一厚度为40mm的无限大平壁，其稳态温度分布为：t＝（180-1800x2）℃。若平壁材料导热系数入＝50W/（m·K），试求：①平壁两侧表面处的热流密度；国【答】②平壁中是否有内热源？若有的话，它的强度是多大？.8【解】①由傅里叶定律：dt林9＝-dx-（-3600x）＝3600x平壁两侧表面的热流密度：运9x＝0＝-入dt＝0dxx＝0dtqx＝8＝-入dx＝40mm＝3600×50×0.04kW/m2＝7.2kW/m2②由导热微分方程：杀界齿类比d2t市两回学的塑平太期＝0dx2入解得dt中＝一入dx＝-入（-3600）＝3600x报＝3600×50W/m3＝1.8×103W/m3人-810/2455。k/s157O0C84％□117：29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.11Size:204×传热学习题集和答案详……传热学习题解答代入微分方程式得：＝a（-2＋4）＝2a＞0aT＝0.y＝1即该导热物体在x＝0，y＝1处的温度是随时间增加逐渐升高。16.试推导圆柱坐标系和球坐标系的导热微分方程。已知物体的导热系数入、密度p和比热容c为常数，且物体内部有均匀稳定的内热源，强度为中。【解】①圆柱坐标系的导热微分方程分析，参见教材图2.5（a）。r方向导热：①＝-rdodzat＝-Adpdzratar币三ar·些早指妈示端d＝-Adodz甲方向导热：中。＝-入drdzapd中。＝-入drdz102do:中茶rapZ方向导热：①2＝-Ardpdrat指应常，厨内天800d中，＝-Ardod22清，高游净导热：衣食项补装肉天常【中a＝-（d中＋d中。＋d中）＋＋由内热源生成热：16（x.8015①。＝Ordodrdz7式中，为内热源强度，W/m3。-10-12/245H田56，l令K/s157084％□17：28P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:4.03Size:188.×传热学习题集和答案详……第2章“导热问题的数学描述”习题解答14.从宇宙飞船伸出一根细长散热棒，以辐射换热形式将热量散发到温度为绝对零度的外部空间，已知棒的表面发射率为，导热系数为入，长度为l，横截面积为A，截面周长为P，根部温度为T。，试写出导热微分方程及边界条件。【解】一对于细长散热棒，假设温度只在杆长方向变化，这属于一维稳态导热问题。分析厚度为dx的微元段的导热：dT，中，＝-入Adx（B）.5器整，谢滚坐圆①。x＋dx＝一入（dT微元段净导热：①＝①-＋＝入Adxdx2中，＝PdxeoTAk一微元段散热量：由能量守恒定律：＝中向式9d2T导热微分方程：＝0dx2AA边界条件：x＝0，T＝T。三计dTx＝l，-入＝E0T4（辐射边界条件）15.无内热源，常物性二维导热物体在某一瞬时的温度分布为t＝2y2cosx。试说明该导热物体在x＝0，y＝1处的温度是随时间增加逐渐升高，还是逐渐降低。【解】常物性无内热源二维物体的导热微分方程式：dt（＋）由某一瞬时的温度分布t＝2y2cosx得：＝01a2（2y2csx）11＝-22cosx0山2a2ta202gy2x＝0，y＝1（2y2c0sx）10.-1＝4c0sx1201＝4—9—11/245H田56l令K/s83.7O0C84％□117：29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.93Size:188×传热学习题集和答案详……第2章“导热问题的数学描述”习题解答内能增量：660:①。＝pcrdodrdata由能量守恒定律：/060mie＋。＝①款约中因导热微分方程：「1旦（，12t，2ar（＇ar/r2az2］pc量前内②球坐标系的导热微分方程分析，参见教材图2.5（b）。r方向导热：安量伯，＝-入rsindprd0ar＋［（＝-Asinat16ar6］＝式感原国检d中＝-入sin0dfdp方向导热：圆出是中。＝-入rd0drat，杀界灯式食变贷回空rsin0ap联意想由。【验】＝-入d0dr1atsin0ap中/6616616shd中。＝一入ddr6sin00方向导热：更。＝-Arsindedratr00＝-入dodrsin0at00:界de＝-入dpdr0sin0atde00净导热：a＝一（d中，＋d中。＋d，）-11-13/245176H田56l令K/s⊙084％117：29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.99Size:188.×传热学习题集和答案详……”传热学习题解答＝Ar？sinOdodedr1a2tar/rsin0do10r2sin0a0sin0at）00家作安园由内热源生成热：:式①。＝r2sinedpdedr内能增量：To（d）2更。＝pcr2sin0dgpd0drar:号回式了由能量守恒：①＋①。＝①-（20）＋山0＋n0品（1heaft1＝0sin0＋ae/lpc17.一具有内热源，外径为o的实心长圆柱体，向四周温度为t的环境散热，表面传热系数为h。试列出圆柱体中稳态温度场的微分方程式及边界条件，并对＝常数的情形进行求解。【解】由题意可知，该圆柱体中的温度只沿半径方向发生变化。其导热微分方程式由61at1a＋（器）＋（1＋得：号回山1d/.d0＋＝0式中，0＝t-to6边界条件：fr＝0deODdr＝0（、-＝r＝To＝002h012-14/245176H田56l令K/s0C84％□117：29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.75Size:179.×传热学习题集和答案详……第2章“导热问题的数学描述”习题解答在常物性，当中＝常数时，原方程积分：人一＝do①r2＋G由：）只。r＝0d＝0一c1＝0公普先对dr再积分：重2＋C20＝一4＋）＋1人＝翼。由：人r＝r0＝2ho＝2h＋4入0三00＝4（-2）＋2h0共受诚由18.一圆筒体的内、外半径分别为r；及ro，相应的壁温为t与to，其导热系数与温度的关系为入＝入o（1＋bt）。试导出计算单位长度上导热热流量的表达式。【解】由题意知，描写上述问题的导热微分方程式可简化为：（r）＝0→（1＋b）］＝0边界条件：6＋）广（）＋＋lr＝ro，tto厨量小高都对方程积分：dt。（1＋b）r＝C三市量内斑元（1＋b）d＝Ao［（-t）＋（-2）］C1In（ro/r；）根据傅里叶定律，求得通过圆筒壁单位管长的导热热流量：13—15/245H田56l令K/s1160C84％□117：29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:2.72Size:179×传热学习题集和答案详……衣传热学习题解答”章《dt91＝-A2Trdr＝-2TC1常＝，踏日＝2m01＋（＋20）m（/）l-10该式与常物性公式形式类似，只是以圆筒壁平均温度tm＝2（t；＋t）计算的导热系数入＝入0［1＋2（4＋t0）］代入常物性公式中进行计算。19.一半径为R的实心球，初始温度为to，突然将其放入液体温度为t的恒温槽内冷却，已知球的导热系数入，密度p和比热容c，球壁表面与液体的表面传热系数h，试写出球体冷却过程的数学描述。【解】由于对称受热，该问题可视为球坐标中的常物性一维无内热源非稳态导热问题。义尚半内藏一8美分析厚度为d的微元球的导热：＝系关0费盛系其①，＝-入（4mr2）民商ar的回牧，联意由【］，-＝-4丌入（r＋dr）2（＋＝-4mA［2＋2rdr＋（dr）2］（0＋山）忽略高阶小量得微元球净导热：中。＝电.-＝4mAr（的＋2）dr微元球内能增量：更。＝pcar42dr由能量守恒定律：＝中。导热微分方程：a＝a1X.2rdr初始条件：r＝0，t＝to边界条件：r＝0＝0（中心无热流，绝热）—14—16/245H田56l令K/s1760C84％□117：29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:2.35Size:163.×传热学习题集和答案详……第2章“导热问题的数学描述”习题解答r＝R，-入＝h（t-t）（第三类边界条件）ar20.设有如图所示的一偏心环形空间，其中充满了某种储热介质（如石蜡类物质）。白天，从太阳能集热器中来的热水使石蜡熔化，夜里冷却水流过该芯管吸收石蜡的熔解热而使石蜡凝固。假设在熔解过程的开始阶段，环形空间石蜡的自然对流可以略而不计，内外管壁分别维持在均匀温度t1及t2。试定性画出偏心圆环中等温线的分布。【解】①（餐式半只面圆进源，才（第20题图偏心圆环中的等温线分布）小21.写出无限长的长方柱体（0≤x≤a，0≤y≤b）二维稳态导热问题完整的数学描述。长方柱体的导热系数为常数；内热源强度为；在x＝0处的表面绝热，x＝a处表面吸收外界温度为t的流体的热量，y＝0处的表面保持恒定温度to，y＝b处的表面对温度为0的流体放出热量。【解】由题意知，该问题的导热微分方程为【贝。（m2t，o2t，①＝0边界条件：x＝0at＝0ax会中客xa，时，大善家丑，＝h（t-）8y＝0，t＝toy＝b，-入at＝ht大量珠早15—17/245HD56l令191K/s084％117:29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:2.72Size:155.×传热学习题集和答案详……第3章“稳态导热”习题解答0变，女1.发生在一个短圆柱中的导热问题，在哪些情形下可以按一维问题来处理？【答】①两端面绝热，圆周方向换热条件相同时，可以认为温度场只在半径方向发生变化；②圆周面绝热，两端面上温度均匀，可以认为温度场只在轴向发生变化。2.扩展表面中的导热问题可以按一维问题处理的条件是什么？有人认为只要扩展表面细长，就可按一维问题处理，你同意这种观点吗？同【答】扩展表面细长，且导热系数大，而表面传热系数相对较小的条件下（hd＜0.01）才可以按一维问题来处理。彩尝入3.在寒冷的北方地区，建房用砖采用实心砖好，还是多孔的空心砖好？为什么？【答】在其他条件相同时，实心砖材料的导热系数约为0.5W/（m·K），而多孔空心砖中充满着静止的空气，空气在纯导热（即忽略自然对流）时导热系数约为0.026W/（m·K）。可见，空心砖是很好的绝热材料。寒冷地区建房用多孔空心砖好。4.冰箱冷冻室内结霜使冰箱耗电量增加，试分析其原因。【答】冰箱中制冷剂在蒸发管内蒸发，吸收冷冻室的热量，使冷冻室降低到指定的温度后，压缩机停止工作。冷冻室内结霜后，蒸发管和冷冻室间增加了一层热阻，制冷剂蒸发温度降低，压缩比增大，耗电量增加。5.平壁与圆筒壁材料相同、厚度相同，在两侧表面温度相同条件下，圆筒内表面积等于平壁表面积，试问哪种情况下导热量大？一16-Y18/245H田56l令K/s1910C84％□117：29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.64Size:196！×传热学习题集和答案详……第3章“稳态导热”习题解答【答】由题意知，平壁导热量：68入A入dl圆管壁导热量：代面两，阳10干语△t0＞8间2ld好，胖量宏井面的大围，图时面头2入d1显丽面泰喝导热量之比：t01个发坛，询10（1＋d人面因中26于会28式曲，更高And，ld，d，m＜1，所以圆筒壁的导热量大。显然，西2母五面，的五母6.冬天，房顶上结霜的房屋保暖性能好，还是不结霜的好？【答】同样的室温条件下，房顶上结霜的房屋保暖性能好，这是因为结霜屋顶的热阻更大，使得其外表面温度较低。7.两根直径不同的蒸汽管道，外表面敷设厚度相同，材料相同的绝热层。若两管道绝热层内外表面温度分别相同，两者每米长的热损失相同吗？高人间。羊一不出重本量用本）【答】：不相同，大管的传热面积大，热损失大。8.如果圆筒壁外表面温度to比内表面温度t高，请定性绘制出壁内的温度分布曲线。1Hm.【答】圆筒壁的温度分布为：t＝4-（i-to）ln二/n2T1071dt＝_-to1＞0三（好m）drIn2r--01＜0＝62H6dr22r2:图-17—19/245H56，l令168K/s⊙C84％□117：29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.65Size:196！×传热学习题集和答案详……传热学习题解答所以，温度分布曲线为单增曲线，且为上凸曲线。山9.工程上采用加肋片来强化传热。何时一侧加肋？何时两侧同时加肋？【答】当传热壁一侧B＜0.1时，该侧加肋可强化传热；当传热壁两侧B都小于0.1时，则两侧都可加肋。加肋时应使壁面两侧表面传热热阻尽量相近，这样强化传热效果好。当壁面两侧均B＜0.1，但一侧表面传热热阻显著大于另一侧表面传热热阻时，在热阻大的一侧加肋效果较好。10.肋片高度增加引起两种效果：肋效率下降和散热表面积增加。因而有人认为，随着肋片高度的增加会出现一个临界高度，超过这个高度后，肋片散热量反而会下降。试分析这一观点是否正确。【答】这一观点是不正确的。计算公式表明，肋片散热量与mH的双曲正切成正比，而双曲正切是单调增加函数，所以散热量不会随高度增加而下降。11.随着肋片的高度增加，换热器的体积、质量和成本增加，换热量也在增加，考虑上述因素应如何确定肋片高度？如果不考虑经济性，肋片是否越高越好？【答】不同材料的体积、质量和成本不一样，不同场合和用途对体积、质量和成本的重视程度也不一样。所以肋片高度的确定标准也不一样。就体积因素而言，对于等截面直肋，耗材∝HA，设：HA＝c（体积不变的情况下），则：国内出本度品hUhUH美曲公盛前内m＝yH，mH＝yHW入A入c0-市伦省卵奇圆【答hU0o中三th（mH）＝hU0oh√yHmH＝hU0oyH整理得：6√yH3＝sh（2yH）—1820/245H56l令225K/sC84％C17:29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.42Size:188×传热学习题集和答案详……第3章“稳态导热”习题解答解此超越方程：√yH3＝1.4192即mH＝1.4192mH是一个无量纲参数，该值表示H与m间的制约关系。不同材料，不同截面形状，不同换热条件，m不同，所以H也不相同。即使不考虑经济因素，肋片也并非越高越好。因为肋片散热量与mH的双曲正切成正比，而双曲正切是以1为极值的单调增加函数，mH＝1.5时其值已超过0.9。12.用热电偶测量某物体的壁面温度，为使测量更加准确，试说明在敷设热电偶时应注意的问题。【答】减少热电偶与壁面的接触热阻；减少通过热电偶线的传热量。13.采用套管式温度计测量流体温度时为什么会产生测温误差？如何减小测温误差？武【答】产生测温误差主要有下列原因：①温度计的感温泡与套管顶部可能存在接触热阻和导热热阻；②套管顶端向根部导热；③套管外表面向流场壁面的辐射换热；④流体与套管外表面的对流换热热阻。稳态时，套管从流体获得的对流热流量正好等于套管向根部的导热和与壁面间的辐射换热量之和。减小测温误差的措施：①加强测温套管附近流场壁面的保温；②采用尽量长的测温套管；③选用导热系数小的材料做测温套管；④在强度允许的情况下，尽量采用薄壁套管；⑤尽量提高流体与套管的对流换热表面传热系数，并注意不使测温套管端部处于流动死角；⑥在不影响对流换热的条件下，在测温套管外安装遮热板以减少与流场壁间的辐射换热。14.一厚为20cm的平壁，一侧绝热，另一侧暴露于温度为30℃的流体中，内热源中＝0.3×10W/m3。对流换热表面传热系数为450W/（m㎡·K），平壁的导热系数为30W/（m·K）。试确定平壁中的最高温度及其位置。01＝【解】由题意知该问题是具有内热源的一维导热问题，其导热微—19—21/245口H56，l令225K/s0C84％117:29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.81Size:188×传热学习题集和答案详……预传热学习题解答分方程为：d？dx＋＝0林园不关厨m好dt＝0x＝0，过州边界条件：x＝8，一入dt＝h（t-t）解微分方程得该平壁内的温度场：019：h更t＝-5000x2＋363.3温度最高处：＝0＝x＝0t＝363.3℃dx15.有一厚为20mm的平面墙，导热系数为1.3W/（m·K）。为使每平方米墙的热损失不超过500W，在外表面上覆盖了一层导热系数为0.12W/（m·K）的保温材料。已知复合壁两侧的温度分别为750℃及45℃，试确定此时保温层的厚度。【解】该问题为多层平壁的导热问题，由教材式（3.12）得：卖长81＝-2-2）＝1750-450.02×0.12m＝0.167m入5001.3回面望味【答】此时保温层的厚度为0.167m。16.一冷藏室的墙由钢皮、矿渣棉及石棉板三层叠合构成，各层的厚度依次为1，150，10mm；导热系数分别为45，0.07，0.1W/（m·K）。冷藏室的有效换热面积为40m㎡，室内外气温分别为-2℃及30℃，室内、外壁面的表面传热系数可分别按3W/（m㎡·K）及10W/（m2·K）计算。为维持冷藏室温度恒定，试确定冷藏室内的冷却排管每小时内需带走的热量。【解】该问题为多层平壁的导热问题，已知：61＝1mm，62＝150mm，63＝10mm，A1＝45W/（m·K），x2＝0.07W/（m·K），入3＝0.1W/（m·K），A＝40m2，i1-2℃，t2＝30℃，h1＝3W/（m2·K），h2＝10W/（m2·K）。则：置其副最端然其同一的妹内具县闻意婆由【】—20—22/245H田56l令K/s109⊙084％117：29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.89Size:179×传热学习题集和答案详……第3章“稳态导热”习题解答t＋00。＋S01.0）中＝A1818281h1A1A2A3h2∥SOST＝＝40×火音30-（-2）8W＝478.3W10.001，0.15.0.01，13450.070.110Q＝＝478.3×3600W＝1721880W17.冷藏箱壁由两层铝板中间夹一层厚100mm的矿棉组成，内外壁面的温度分别为-5℃和25℃，矿棉的导热系数为0.06W/（m·K）。求散冷损失的热流密度q。大气水分渗透使矿棉变湿，且内层结冰。设含水层和结冰层的导热系数分别为0.2W/（m·K）和0.5W/（m·K），问冷藏箱的冷损失增加多少？【解】①由热阻分析，两层铝板热阻可以忽略不计，干燥时冷损失为：）同q＝入三（25＋5）0.1×0.06W/m2＝18W/m218②假设环境温度30℃，相对湿度70％，对应露点温度ta＝23.3℃，结冰厚63，含水层厚62，千燥层厚61，61＋62＋63＝0.1m。此条件下的热损失为：（t-5）q＝即q61＝入1（t1-t2）＝0.102W/m（2一）名q＝i即q2＝入2（t2-t3）＝4.66W/mE83（t-t4）1-）-0q＝83e-0×850即qo3＝入3（t3-4）＝2.5W/m981＋982＋q83＝q8，解得：.0-21-23/245H56，l令242K/s⊙084％117：29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.91Size:188.×传热学习题集和答案详……冬沙传热学习题解答9≈（0.102＋4.66＋2.5）W/m0.1m＝72.62W/m1该损失是原散热量18W/m㎡的4.03倍。所以，保温材料需采取防潮、防水措施。0018.假定人体对冷热的感觉以皮肤表面的热损失作为衡量依据。设人体脂肪层的厚度为3mm，其内表面温度为36℃且保持不变，无风条件下，裸露的皮肤外表面与空气的表面传热系数为15W/（m2·K）；有风时，表面传热系数为50W/（m2·K），人体脂肪层的导热系数为0.2W/（m·K）。试确定：①要使无风天的感觉与有风天气温-15℃时的感觉一样，则无风天气温是多少？②在同样是-15℃的气温下，无风和刮风天，人皮肤单位面积上的热损失之比是多少？【解】①该题目可视为第三类边界条件下的平壁导热问题（不考虑辐射散热）。无风天的感觉与有风天气温-15℃时的感觉一样，皮肤散热量应相等，当不考虑辐射散热时，应有：t-t有风tw-t无风6，16，1Ah风Ah无风（-）61入h无风（t-有风）03），人＝160喝t无风＝t-81入h有风3×10-31＝36-0.215［36-（-15）］℃＝-83℃3×10-3，10.25061m3×10-3，19元风入h有风0.250＝0.439凤8，13×103，1供入h风0.215—22—24/245H56，l令242K/s084％117:29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:4.05Size:179.×传热学习题集和答案详……第3章“稳态导热”习题解答19.为测量某种材料的导热系数随温度的变化规律，取厚度为50mm的无限大平壁试样，稳态时测得：材料两侧的温度分别为100℃和20℃，中心面的温度为50℃，热流密度为500W/m㎡，试确定该材料导热系数随温度的关系入＝入o（1＋bt）中的常数入o和b。【解】稳态且当导热系数随温度的变化规律已知时，可得：:（98/25000.025t1-m100-50011＋（＋＝入o（1＋75b）＝0.25【藏1入298/2500×0.025tm-t250-20A01＋（＋＝入o（1＋35b）＝5/12解两式得：9Ao＝16b＝1135:鼎平塑20.外径为50mm的蒸汽管道外，包覆有厚为40mm，平均导热系数为0.11W/（m·K）的矿渣棉，其外为厚45mm，平均导热系数为0.12W/（m·K）的煤灰泡沫砖。绝热层外表面温度为50℃。试检查矿渣棉与煤灰泡沫砖交界面处温度是否超过允许值300℃。另外，增加煤灰泡沫砖的厚度对热损失及交界面处的温度有什么影响？蒸汽管道的表面温度取为400℃。【解】该问题为第一类边界条件下的多层圆筒壁导热问题，由教材式（3.24）整理变形可得：t1入1ln（r3/r2）＋t3入2ln（r2/r1）2A1In（r3/2）＋A2ln（r2/1）一400×0.11xn（110/65）＋50×0.12xn（65/25）C0.11×ln（110/65）＋0.12×ln（65/25）＝167.4℃×m80该温度在两保温材料的允许使用温度范围内，增加泡沫砖厚度能降低热损失，交界面处的温度会上升。21.一蒸汽锅炉炉膛中的蒸发受热面管壁受到温度为1000℃的烟气加热，管内沸水温度为200℃，烟气与受热面管子外壁间的复合-23-25/245HD56，l令216K/s0C84％□117：29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:2.08Size:188×传热学习题集和答案详……传热学习题解答换热表面传热系数为100W/（m㎡·K），沸水与内壁间的表面传热系数为5000W/（m2·K），管子外径为52mm，壁厚6mm，管壁导热系数入＝42W/（m·K）。试计算下列3种情况下受热面单位长度上的热负荷和管壁平均温度：中（＋）o人二人关品的号①换热表面无垢；财变阳更图止态】②外表面结了一层厚为1mm的烟灰，其入＝0.08W/（m·K）；③内表面上有一层厚为1mm的水垢，其入＝1W/（m·K）。【解】①换热表面无垢时，热负荷：t，-0q＝W/m1In（ro/r；）12r:h:2TAg2Troho＝12539W/m粉左两精管壁平均温度：91t；＝2mr；hi＋t，＝125392T×0.02×5000＋200）℃＝220℃1012539蓝to＝ty91＝（1000-）℃2Troho2×0.026×100，＝232℃产tm＝（to＋t；）/2＝（232＋220）/2℃＝226℃②外表面结了一层厚为1mm的烟灰时，其热负荷为：爆山t.-t91＝面变（毛）材1（）（）2rh；2m入g2m入2mr，ho1000-200-W/mxIn26202T×0.02×5000＋2m×42＋2T×0.08＋2m×0.027×100＝5856W/m量，内国更岳甲势单能朵盐管壁平均温度：代工会的面界交，夫味外阳3，00019i＋t受塑5856t℃＋200℃＝209℃合豆2mr；his面2m×0.02×5000一24—26/245才K口H田56l令K/s216⊙084％17：29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.15Size:204.×传热学习题集和答案详……第3章“稳态导热”习题解答变取（E.￡）1nToIn2610＝＋912＝（209＋5856202m×42℃＝215℃tm＝（to＋t）/2＝（215＋209）/2℃：＝212℃大系③内表面上有一层厚为1mm的水垢时，热负荷：115t，-t，91三人Inlno人12mr，h；2入，2m入g2Tr，ho0011.01000-200面：KIn20In2611902m×0.019×5000＋2m＊1＋2m42＋2m0.026×100＝11104W/m管壁平均温度：821.0000to＝t一2troho911000℃111042T×0.026×100℃新F320℃，感果y恭，蛋m0＝b代一ES排林，0式1no养代其，上阳m20.0取园一国T国t＝to-9i2＝320℃-11104xln（26/20）2丌×42℃装号8＝309℃）W，0三人爱m20.0圆tm＝（to＋t）/2＝（320＋309）/2℃内.08式实康面东＝315℃人持想可见，不论结水垢还是灰垢都会使热负荷下降，而结水垢还会使管壁温度上升，造成安全隐患。22.某管道外径为2，外壁温度为t1，外包两层厚度均为6（62＝83＝），导热系数分别为入2和入3（入2＝2入3）的保温材料，外层外表面温度为2。如将两层保温材料的位置对调，其他条件不变，保温情况如何变化？由此能得出什么结论？【解】该问题为第一类边界条件下的多层圆筒壁导热问题。设2527/245HD56l令114K/s⊙084％117：29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:2.63Size:171.×传热学习题集和答案详……传热学习题解答各层直径分别为d1，d2，d3，＝2.d33由教材式（3.32）整理变形可得：导热系数大的在里面：了S（00S＋16）＝:t-t2木的mml是△t1面志内⑧9n＝d21-Ind31-In211.32m入2d12m入3d22m·2入32T入32入3△t0.11969导热系数大的在外面：00一0001△tn入3△t92＝001n2＋130.14258000元2m入32m2入329n_0.142589n0.11969＝1.19结论：在保温厚度相等的条件下，导热系数大的材料放在外层对保温更有利，同等条件下可减小热损失19％。23.一外径do＝0.3m的蒸汽管道，蒸汽温度为400℃。管道外包了一层厚0.065m的材料A，测得其外表面温度为40℃，但材料A的导热系数无数据可查。为了知道热损失情况，在材料A外又包了一层厚0.02m，导热系数入B＝0.2W/（m·K）的材料B。测得材料B的外表面温度为30℃，内表面温度为180℃。试推算未包材料B时的热损失和材料A的导热系数入Ao【解】蒸汽凝结传热热阻和金属壁导热热阻可以忽略，对于绝热材料B:2丌g（tgi-tg。）2×0.2（180-30）91＝WdBo0.3＋0.065×2＋0.02×2In息代拌林梁dn）人0.3＋0.065×2彩，变不＝2119W/m置阳林慧朵昆林长实新面含公出由变回只前盛货回转长塑圆金的不杀界类一比回【—26—28/245口H56，l令227K/s⊙084％117：29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:2.48Size:163.×传热学习题集和答案详……第3章“稳态导热”习题解答则：入n（dn/dn）-21191n（0.43/0.3）W/（m·K）勇女Am2m（tA产tB）T2T（400一180）2代夹＝0.552W/（m·K）来夹的3长夏快景未包材料B时的热损失：的特乳，园断mo0到星合女国2丌入A（tn-tA）2丌×0.552×（400-40）阳天广9i＝daoW/m0.43装I夹就）量容d0.3前变盛子0韩一＝3468W/m。（不面塑的避24.在我国南方某地建一室内制冷装置，其工作温度为-40℃，采用微孔硅酸钙制品做隔热材料。该地区最热月份的平均温度为30℃，相对湿度为85％，对应的露点t＝27.4℃。该装置的管道外径为108mm。设计时取绝热材料层外表面温度比露点高1.5℃，绝热材料层外表面的表面传热系数为8.14W/（m2·K）。求绝热层厚度8。【解】由热阻分析隔热层内表面温度可近似为-40℃，隔热层外表面温度高于露点1.5℃，即to＝（27.4＋1.5）℃＝28.9℃。隔热层平均温度：tm＝（28.9-40）/2℃＝-5.55℃（S查教材附录2，微孔硅酸钙制品导热系数：阳补热宝入＝0.041＋0.0002t＝［0.041＋0.0002×（-5.55）1W/（m·K）＝0.04W/（m·K）由：杀界成类一草成91＝te-tw（ta-ta）＝d2d21d22A.tm2-twl0.108h2t-tw22×0.04、28.9-（-40）8.141＝0.61630-28.9-27—29/245H56，l令227K/s⊙084％117：29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.70Size:188！×传热学习题集和答案详……雅族传热学习题解答幸采用图解法或试算法求得：d2＝0.438me16＝0.165mml25.有一批置于室外的液化石油气储罐，内直径为2m，通过使制冷剂流经罐外厚为1cm的夹层来维持罐内的温度为-40℃。夹层外是厚为30cm的保温层，保温材料的导热系数为0.1W/（m·K）。在夏天的恶劣条件下，环境温度为40℃，保温层外表面与环境间的复合换热表面传热系数可达30W/（m2·K）。试确定为维持液化石油气-40℃的温度而对该球罐所必须配备的制冷设备的容量（罐及夹层钢板的壁厚可略而不计）。、了【解】该问题为第三类边界条件下球体的一维稳态导热问题，罐体本身的热阻可忽略不计。由题意知，为维持罐内液化石油气温度为-40℃，夹层内制冷剂的蒸发温度也必须是-40℃，即保温层与夹层接触面的温度tm1＝-40℃。设环境温度为t，则制冷设备的容量为：4-WH.8造滚鼎面赤阳面素代是排＝1/-1/5214T入妹，子0外4Tr2h内县形仪围瘀由【】40-（-40）W＝439.6W1/1.01-1/1.314m×0.14m×1.312×30平恩副定导热系数球体的一维稳态导热的微分方程式（见教材式2.12）1000.0＋10.0＝1可简化为：·m）W（2-）×000.0＋1H0.01dr＝0·m）NW0.0由如为第一类边界条件r＝T1，t＝twl，可解得：lr＝r2，t＝t2三dt1tw-t2dr-r21/r2-1/1sb（1）4丌入（t-t2）重＝1/-1/2（0p-）-e，8.0880100＝.8S-0818-28-30/245口H田56l令K/S144⊙084％117：29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.23Size:188×传热学习题集和答案详……第3章“稳态导热”习题解答r＝ri，t＝twl该题的边界条件为r＝T2，-入rre业＝h（ta-），结合式（1）可得：dro∮＝4丌入（tm1-t2）20＝Sh＝mm1/r1-1/r2c.S＝H＋＝（2）更＝h4mr2（tm2-t），Sip.2＝联立求解式（2），消去未知的t2可得：×8000.0＝3＝A01X80.F×dOI（三（）八H）1/T1-1/2，0＝1蜡接，8.04m入率4r2h等81E查26.试计算下面两种尺寸相同的等厚直肋的肋效率，肋高H＝25mm，厚度6＝1mm，表面传热系数h＝35W/（m2·K）:①铝肋：导热系数入＝207W/（m·K）；-②钢肋：导热系数入＝41.5W/（m·K）。【解】①铝肋：然始管即米2h00012）＋000「2x35m＝V入6207×0.001m-1＝18.39m-10001H＇＝H＋6/2＝（25＋1/2）mm＝25.5mmcmH’＝18.39×0.0255＝0.469005）×O1x20.0_th（mH＇）_th0.469me＝0.93mH＇0.469世m②钢肋：直纯炎暖我，系装皂的闻金某换大8已12h2x35一，金m＝VA8＝41.5×0.001m＝41.07mm＝面券的间」mH＇＝41.07×0.0255＝1.047_th（mH＇）th1.047mi＝0.746亲早金效mH＇1.047联意由【鞭】27.在外径为25mm的管壁上装有铝制的等厚度环肋，相邻肋片中心线之间的距离s＝5mm，环肋高H＝12.5mm，厚6＝0.8mm。管壁温度tw＝200℃，流体温度tg＝90℃，管基及肋片与流体之间的表面传热系数为110W/（m2·K）。试确定每米长肋片管（包括肋片及基—29—31/245H田56l令K/S144⊙084％□117：29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.98Size:188.×传热学习题集和答案详……传热学习题解答幸管部分）的散热量。:【解】查教材表2.1得铝的导热系数入＝236W/（m·K），则：H＇＝H＋6/2＝（12.5＋0.8/2）mm＝12.9mmT1＝d/2＝25/2mm＝12.5mm（r2＝r1＋H＇＝12.5mm＋12.9mm＝25.4mmr2/1＝25.4/12.5＝2.032mA＝小A，＝6H＇＝0.0008×0.0129m2＝1.032×10m2（H）32［h/（入A）］2＝（0.0129）32［110/（236×1.032×10）］2＝0.309查教材图3.18得环肋的效率＝0.89，则每片肋散热：＝2（r3-r）h（t-t）ne同麻七贝特面货＝2×3.14（0.02542-0.01252）×110×（200-90）×0.89W＝33.1W每米肋片管散热：（X·m）NWC.I＝大基号：⑧1三1000＋（1-1008）rdh（t.-）m0E.81＝103081＋11-1001000×0.0008×3.14×0.025×110×（200-90）W/m0×0E81＝Hm3F00＝7415W/m28.为测定某金属的导热系数，进行如下实验。取直径为20mm的金属长棒，一端放入炉中加热，另一端伸到20℃的空气中，空气与棒之间的表面传热系数为12W/（m2·K）。达到热稳态后，在相距100mm的两截面上测得温度分别为t1＝120℃，t2＝60℃。试确定该金属的导热系数。Hm【解】由题意知，该题目可视为无限长细杆传热问题。＝e-m（1-2），得：028.0＝8【＝H高眼不，mm乙＝离间中面泰的面尚已超义，工、0Q0，9005＝1塑m（x-x2）＝-In基代烟）汽曲冠02）八70式钱—30—32/245HD56，l令213K/s⊙084％117：29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.88Size:180.×传热学习题集和答案详……第3章“稳态导热”习题解答即m×0.1＝-1n60-20120-20＝0.9163m＝9.163＝hU4h4×12NA×0.02入＝28.6W/（m·K）29.一根外径为25mm，外表面温度为120℃的管子上，沿周向均匀布置12根纵肋。肋厚为2.5mm，肋高19mm。肋片导热系数为111W/（m·K），空气温度为27℃，表面传热系数为20W/（m2·K）。试求加肋后该管的换热量与未加肋时换热量之比。【解】m＝2h2×20-V入8V111×0.0025m7＝12.0m-1H＇＝19mm＋2.5/2mm＝20.25mm→＞mH＇＝12.0×0.02025＝0.243单位管长每片肋片的散热量：xH＝0更＝入Am0th（mH＇）c＝111×0.0025×12×（120-27）th0.243W＝73.8W）3加肋后单位管长散热量：（0os）2o-（Hm）d中1＝12xp＋h（md-126）（t-t）（＝12×73.8＋20×（3.14×0.025-12×0.0025）×（120-27）W/m＝976W/m刘未加肋时的换热量：迷。泰早持林出区用味花＝h（d）（t-t）长爽康本，中本一同氏置牙眼长变盛＝20×（3.14×0.025）×（120-27）＝146W/m9001加肋后换热量与未加肋时换热量之比：30＝n.5＝，长中1976＝6.68①1460意由【臧】30.为测定管道内蒸汽的温度，在管道壁安装了套管温度计，套管直径为20mm，长70mm，壁厚2mm，套管材料导热系数为46.5W/（m·K），蒸汽管道壁温为50℃，蒸汽与套管间的对流换热表面传-3133/245H56，l令216K/s00C84％117:29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.85Size:188×传热学习题集和答案详……谷传热学习题解答幸热系数为116W/（m2·K）。若温度计指示温度为155℃，试确定蒸汽的真实温度。【解】套管温度计可视为一个空心等截面直肋，由于温度计的感温泡与套管顶部直接接触，可以认为温度计的读数就是套管顶端的壁面温度t。温度计套管与周围环境之间存在着3种方式的热量传递：①通过套管壁从端部向基部的导热；②与蒸汽之间的对流换热；③与蒸汽管内壁面之间的辐射换热。稳态时，对流换热获得的热量应等于导热量和辐射换热量。因此，套管端部温度必然低于蒸汽温度，这就是存在测温误差的原因。A＝（-）＝［（0.02）2-（0.016）3m210S0.0＝1.13×104m2m2，09＝mnN，9＋mme1＝HEA00＝116×T×0.02mH＝×0.07V入A46.5×1.13×10习普分单＝2.607（Hm）dmA人＝①E.0（T9t-tX1×2900.0x1＝tH-tr＝ch（mH）tach（mH）-to155ch（2.607）-50蜡营动单司地℃＝173℃ch（mH）-1ch（2.607）-1）＋1＝4173-1551）×0＋8.E×S1＝E＝×100％＝10.4％173Te＝mv（T-0131.利用对比法求材料导热系数。将直径相同的A，B两种材料做成的细长杆置于同一流体中，流体温度为25℃。将两杆安装于温度为100℃同一表面上。同时测得离开该表面相同距离的两杆上的温度分别为t＝75℃，t＝65℃。已知材料A的导热系数为200W/（m·K），求材料B的导热系数。【解】由题意知0A＝00emx，0＝0oem，则：mA_ABn（0n/00）ln［（75-25）/（100-25）＝0.645mg-NAA-In（B/00）-ImL（65-25）/（100-25）AB＝AA×0.6452＝200×0.6452W/（m·K）＝83.2W/（m·K）-32-34/245才K口H田56l令K/s292⊙084％117：29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.67Size:196！×传热学习题集和答案详……传热学习题解答蓝期面0.752＋4×0.75×0.5-5.84（0.75＋0.5）＋6.12809008内.（，m）80条提，m计0082.06257.3＋6.128＝56.25塑意面三果。齿式的业夫母肤个一出6＝0.0327m34.外径为60mm，表面温度为200℃的蒸汽管道，外绝缘层为边长100mm的正方形截面，绝热材料导热系数为0.1W/（m·K）。绝热层外表面温度为50℃。试计算每米长管道的热损失。若用同样多的材料做成圆形截面，热损失又是多少？【解】绝热层为正方形时，该导热过程的形状因子：402丌2×3.14S，＝m＝10.69m由【（1.08×）m（1.080.10.060＝881.0＝单位管长散热损失：8.0100＝（）Ke＝91＝s1A（t1-t2）＝＝10.69×0.1×（200-50）W/m5.0xm0＝160.4W/m若用同样多的绝热材料做成圆形截面，则：面更中其，式立的m；（才·N10.0塑代，301-式4d3＝b2各县式人领面的室4已且婚。30式进d2＝VW补亦夫最型要，（0·世）八V0，0＝A，4×0.120＝120＝n1】m＝0.113mT1-）-390＝12丌入（t1-t2）91＝In（d21d）＝02x50.02丌×0.1（200-50）＋（3-0）＋x2元0ln（0.113/0.06）W/m-0）＝2＝148.8W/m0＋（6-d）＋×2.0851.0＋（d＋）B.一-34-36/245H田56l令K/s2160C84％□17：29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:4.13Size:188.×传热学习题集和答案详……第3章“稳态导热”习题解答32.如图所示，试计算通过一立方体墙角的热损失，已知每面墙厚300mm，导热系数为0.8W/（m·K），内、外壁温分别为400℃及50℃。如果三面墙的内壁温度tu，t2，t1各不相等，但均高于外壁温度，试提出一个估算热损失范围的方法。m7S80.0＝2d或火氢的州，斯普燕18容，1a00试酸。（·m）八W0，面讯式m001金料同田等。夫处妹文夫，面进圆州干因（第32题图）【解】由表3.2（见教材）查得该条件下导热过程的形状因子：s＝0.156＝0.15×0.3＝0.045中＝s入（t1-t2）＝0.045×0.8×（400-50）W立单＝12.6W人、＝D估算热损失时，用三内壁平均温度作为内壁温度。33.一冰箱的冷冻室可看成是外形尺寸为0.5m×0.75m×0.75m的立方体，其中顶面尺寸为0.75m×0.75m。冷冻室顶面及4个侧面用同样厚度的发泡塑料保温，其导热系数为0.02W/（m·K）；冷冻室的底面可近似地认为是绝热的。冷冻室内壁温度为-10℃，外壁护板温度为30℃。设护板很薄且与发泡塑料接触良好。试估算发泡塑料要多厚才可限制冷量损失在45W以下。【解】a＝0.75m，b＝0.5m，＝45W，入＝0.02W/（m·K），△t＝30℃-（-10）℃＝40℃。更45（一）人mS入t0.02×40＝56.25b）三s＝（a-28）244（a-28）（b-6000＋0.54×4（a-28）＋0.54×4（b-6）＋0.158×481a2＋4ab-5.84（a＋b）＋6.1288-33-35/245口H56，l令292K/s⊙84％117:29P:0/1dX:-0.5dY:0.5Xv:0.0Yv:0.0Prs:1.29Size:196.×传热学习题集和答案详……一个装早第4章“非稳态导热”习题解答函1.什么叫非稳态导热的正规状况阶段？这一阶段有什么特点？【答】非稳态导热过程进行到一定程度，初始温度分布的影响就会消失，虽然各点温度仍随时间变化，但各点过余温度的比值已与时间无关，亦即无量纲过余温度分布不变，这一阶段称为正规状况阶段或充分发展阶段。这一阶段的数学处理十分便利，温度分布计算只需取无穷级数的首项进行计算。，口来谷］科2.试说明“无限大”平板的物理概念，并举出一两个可以按无限大平板处理的非稳态导热问题。域盏润变【答】所谓“无限大”平板，是指其长宽尺度远大于其厚度尺寸，从边缘交换的热量可以忽略不计，当平板两侧温度均匀时，热量垂直于板面方向流动。如薄板两侧均匀加热或冷却，以及炉墙或冷库的保温层导热等情况可以按无限大平板处理。3.有人认为，当非稳态导热过程经历时间很长时，采用诺谟图计算所得的结果是错误的。其理由是：诺谟图表明，物体中各点的过余温度的比值仅与几何位置及有关，而与时间无关。但当时间趋于无限大时，物体中各点的温度应趋近流体温度，所以两者是有矛盾的。你是否同意这种看法？请说明其理由。素分一，人最【答】这种看法不正确，因为随着时间的推移，虽然物体中各点过余温度的比值不变，但各点温度的绝对值在无限接近。这与物体中各点温度趋近流体温度的事实并不矛盾。度内皮的要主4.什么是“半无限大”物体？半无限大物体的非稳态导热存在正规状况阶段吗？【答】所谓“半无限大”物体，是指平面一侧空间无限延伸的物体。因为物体向纵深无限延伸，初始温度的影响就远不会消除，所以半无限大物体的非稳态导热不存在正规状况阶段。内【】—35—37/245H56，l令191K/s◎084％117：29P:0/1dX:-3.0dY:1.5Xv:-0.185Yv:0.087Prs:3.16Size:171.×传热学习题集和答案详……传热学习题解答5.什么是非稳态导热问题的乘积解法，该解法使用条件是什么？【答】对于二维或三维非稳态导热问题的解等于对应几个一维问题解的乘积，其解的形式是无量纲过余温度，这就是非稳态导热问题的乘积解法。其使用条件是恒温介质，第三类边界条件或边界温度为定值、初始温度为常数的情况。6.本章的讨论都是对物性为常数的情形作出的，对物性是温度函数的情形，你认为应怎样获得其非稳态导热的温度场？非容讯【答】出应用变物性微分方程进行分析求解。盛谷然量会7.结合非稳态导热分析解的形式，分析热扩散率在非稳态导热中的作用。食更，味长十学麦如一【答】从分析解形式可见，物体的无量纲过余温度是傅里叶数的负指数函数，即表示在相同尺寸及换热条件下，热扩散率越大的物体到达指定温度所需的时间越短，这正说明热扩散率所代表的物理含义。其干天贝其最，平大天“【谷】直8.由导热微分方程可见，非稳态导热只与热扩散率有关，而与导热系数无关。你说对吗？（提示：导热的完整数学描述为导热微分方程和定解条件）竹【答】上述观点不对。因为热扩散率中含有导热系数，而且导热问题的完整数学描述不仅包括控制方程，还包括定解条件，第二或第三类边界条件中都隐含着导热系数的影响。置面回儿外的福9.试说明Bi数的物理意义。Bi一→0及Bi一→∞各代表什么样的换热条件？有人认为，B一→0代表了绝热工况，你是否赞同这一观点，为什么？本然虽，间因不去【谷【答】岁Bi数是物体内外热阻之比的相对值。Bi→O时说明传热热阻主要在边界，内部温度趋于均匀，可以用集总参数法进行分析求解；B一→∞时，说明传热热阻主要在内部，可以近似认为壁温就是流体温度。认为Bi→0代表绝热工况是不正确的，Bi一→0的工况是指边界热阻相对于内部热阻较大，而绝热工况下边界热阻无限大。容四10.试说明集总参数法的物理概念及数学上处理的特点。本【答】当内外热阻之比趋于零时，影响换热的主要环节是在边界36—38/245口HD56，l令191K/s84％117:29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.26Size:204.×传热学习题集和答案详……第4章“非稳态导热”习题解答上的换热能力，而内部由于热阻很小而温度趋于均匀，以至于不需要关心温度在空间的分布，温度只是时间的函数，数学描述上由偏微分方程转化为常微分方程，大大降低了求解难度。11.什么叫时间常数？试分析测量恒定的流体温度时。对测量准确度的影响。【答】具有时间的量纲，称为时间常数，。数值上等于过余温hA度为初始过余温度的0.368时所经历的时间。T。越小，表示物体热惯性越小，到达流体温度的时间越短。测温元件的时间常数大小对恒温流体的测量准确度没有影响，对变温流体的测量准确度有影响，。越小，准确度越高。12.在用热电偶测定气流的非稳态温度场时，怎样才能改善热电偶的温度响应特性？【答】要改善热电偶的温度响应特性，需最大限度降低热电偶的时间常数，形状上要降低体面比，要选择热容小的材料，要强化热电偶表面的对流换热。13.在某厂生产的测温元件说明书上，标明该元件的时间常数为1s从传热学角度，你认为此值可信吗？【答】根据时间常数定义＝hA，在一定条件下p，c，V，A可以认为是常数，但表面传热系数h却是与测温元件与被测物的换热条件有关。因此，对该说明书上表明的时间常数值要进行具体分析，不能盲目相信。14.一块无限大平板，单侧表面积为A，初温为o，一侧表面受温度为t，表面传热系数为h的气流冷却，另一侧受到恒定热流密度qw的加热，内部热阻可以忽略。试列出物体内部的温度随时间变化的微分方程式并求解之。设其他几何参数及物性参数已知。【解】由题意知，物体内部热阻可以忽略，温度仅为时间的函数，一侧的对流换热和另一侧恒热流加热作为内热源处理，根据热平衡可得控制方程为：意的交节奥感中出画贷泰-37—39/245口HD56，l令248K/s0C84％□117：29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.11Size:188！×传热学习题集和答案详……茶传热学习题解答幸下pcV＋hA（t-1）-Ag＝0科千由酷内面，菌dr初始条件：t，＝o＝o的来了升大大，联式公贵常式3pcVde引入过余温度0＝t-t，则：dr＋hA0-Ag＝0＝0＝to-t＝00余上述控制方程的通解为：O＝BexphA9pcv）t量由初始条件有：B＝一w联站间的度酯科，小指量派故温度分布：0＝00exp）91-0（-115.设有5块厚30mm的无限大平板，各用银、铜、钢、玻璃及软木做成，初始温度均匀（20℃），两侧面突然上升到60℃，试计算使中心温度上升到56℃时各板所需的时间。5种材料的热扩散率依次为170×10-6，103×10-6，12.9×10-6，0.59×10-6，0.155×10-6m2/s。由此计算你可以得出什么结论？O＝1m-G＝56C-60℃＝-4℃0＝0.1某【解】l0o＝to-t＝20℃-60℃＝-40℃00由第一类边界条件：B一→∞→1＝m/2嫂常回【容］代入平板中心无量纲过余温度：0n（r）2sinB味系面春团，嫂常县肉0。B1＋sinB，cosB-exp（-BFo）＝Fo＝1.0311.031822.3198×10-4。目又6＝0.03/2＝0.015，7＝0a依次代入5种材料的热扩散系数后得银、铜、钢、玻璃及软木板中心温度到达56℃的时间分别是：1.36，2.25，17.98，393.18，1496.61s。可见，到达相应温度的时间与热扩率成反比。几其好永张发16.设一根长为l的棒有均匀初始温度to，此后使其两端各维持在恒定的温度t1（x＝0）及t2（x＝l），并且t2＞t1＞to。棒的四周保持绝热。试画出棒中温度分布随时间变化的示意性曲线及最终的温度分38—40/245才K229084％C□117：29P:1/1X:762.0Y:35.5Xv:0.0Yv:0.544Prs:4.23Size:179.×传热学习题集和答案详……麒传热学习题解答上由0o＝exp（-Bi·Fo）Fo＝aT曲82贝曲亦代变盛［治】，00解得T＝82aBi0（4×10-3）2-15-257.5×10-7×1.6×10-2m10-25＝1308s即等待1308s以后，瓷砖温度才能上升到10℃。当瓷砖厚度增加1倍，其他条件不变时：式好平大氏oBi2h8＝3.2×102＜0.1入001（8×10-3）2-15-2587.5×10-7×3.2×10-210-25s＝2615s19.位于寒冷地区的一大直径输油管的外径为1，壁厚45mm，油管外侧绝热良好。未送油前油管温度为-20℃，然后80℃的热油突然流经该油管，与内壁间的表面传热系数h＝400W（m㎡·K）。试确定：①输油5min后油管外表面的温度；②输油5min后内表面的瞬时热流密度；③输油5min内油管单位长度上所吸收的热量。输油管的入＝43W/（m·K），a＝1.17×10-5m2/s。0、0【解】由题意知输油管长度、周长远大于其厚度，由于输油管外侧绝热，以绝热面作为对称面，可把该问题视作半厚6＝45mm的无限大平壁的非稳导热。Bi＝h6_400x45x103D-入-43面＝0.4186＝B1＝0.6051ar_1.17x10-3x5x60Fo＝＝1.7333＞0.282c＝（0.045）2①输油5min后油管外表面的温度：助（：0m2sinB式exp（-BFo）0.B，sinB，cosBi2×0.56880.6051＋0.5688×0.822exp（-0.60512×1.7333）—4042/2450中H田56l令K/s137⊙084％117：29P:0/1dX:2.0dY:0.0Xv:0.154Yv:0.0Prs:1.75Size:188.×传热学习题集和答案详……（传热学习题解答由000＝exp（-Bi·Fo）Fo＝aT82曲市代盛［治】解得T＝8200aBi0（4×10-3）2-15-25n7.5×10-7×1.6×10-210-25＝1308s即等待1308s以后，瓷砖温度才能上升到10℃。当瓷砖厚度增加1倍，其他条件不变时：好平大用一oBi2h8＝3.2×102＜0.1入0分01×（8×10-3）2-15-257.5×10-7×3.2×10-210-25s＝2615s19.位于寒冷地区的一大直径输油管的外径为1m，壁厚45mm，油管外侧绝热良好。未送油前油管温度为-20℃，然后80℃的热油突然流经该油管，与内壁间的表面传热系数h＝400W/（m㎡·K）。试确定：①输油5min后油管外表面的温度；②输油5min后内表面的瞬时热流密度；③输油5min内油管单位长度上所吸收的热量。输油管的入＝43W/（m·K），a＝1.17×10-5m2/s。【解】由题意知输油管长度、周长远大于其厚度，由于输油管外侧绝热，以绝热面作为对称面，可把该问题视作半厚6＝45mm的无限日n8大平壁的非稳导热。Bi＝h6_400x45x10325D-入-43面＝0.4186→B1＝0.6051ar_1.17x10-3x5x60Fo＝1.7333＞0.282c＝（0.045）2①输油5min后油管外表面的温度：时（m0m2sinBexp（-BFo）0.B，sinB，cosBi2×0.56880.6051＋0.5688×0.822exp（-0.60512×1.7333）—40—42/2455。k/s137⊙084％117：29P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:4.48Size:188.×传热学习题集和答案详……第4章“非稳态导热”习题解答＝0.5621顶意婆由破回州tm＝0.5621×（-20-80）℃＋80℃＝23.8℃②输油5min后内表面的瞬时热流密度：02sinB0oexp（-BiFo）axBsinBicosB［-（）00B12sinBiY（＝一sinBi8exp（-BFo）BsinB，cosB0mB1sinB，＝（23.8-80）×0.6051sin0.6051（m）八10.045县＝429.88000试溶，，1S9＝＝43×429.88W/m2＝18485W/m2axx＝8③输油5min内油管单位长度上吸热量：05.Q＝Q0［10002sinpBi（B，sinB，cosB，rexp（-B:Fo）A·m）W2sinBexp（-BFo）变感B，（BsinB，cosB80112sinBB（B，sinB，cosB）exp（-B；Fo）435×1×0.045（-20-80）841.17×101-0.64920.6472p（-0.6347）J/m否，201场不间0001.0号＝-2.45×107J/m2.用常功率平面热源法对材料的导热系数进行测定，所测试件可被视为一半无限大物体。平面热源的功率为60W/m2。如试件初始温度为15℃，通电加热后，经过300s试件与平面热源接触表面处温度测得为20℃，经过360s，测得距平面热源0.015m处试件的温度为16.673℃。试求该材料的导热系数。【解】该题目为第二类边界条件下的半无限大物体的非稳态导—4143/245才KH田56l令K/s177⊙0C84％□17：30P:0/1dX:-0.4dY:0.2Xv:-0.023Yv:0.015Prs:1.58Size:196.×传热学习题集和答案详……谷轴传热学习题解答热问题。由题意可得：82082qw0.（T1）＝aT1082×603000（20-15）℃＝5℃入V丌AV丌29warierfe（）m0（x，T2）＝2/aT282008＋80（x，T2）＝2×60√360aierfc（0.015）＝（16.673-15）℃入2/360a1200.0＝1.67℃0x（08-8:）以上两式联立求解得入＝0.1656W/（m·K）21.冬天，太阳对地面的辐射热流密度为600W/m2，河面冰层对太阳光的吸收率假定为0.6，冰层很厚，但初始温度仍均匀为-15℃。试问太阳照射多久以后冰层表面才开始融化？【解】该题目为第二类边界条件下的半无限大物体的非稳态导热问题。由教材附录1查得冰的p＝920kg/m3，入＝2.26W/（m·K），c＝2.26kJ/（kg·K）。冰层表面才开始融化时冰层表面温度要大于等于0℃。ames八0（T）29.ar_2×600×0.62.26T℃V丌2.26920×2.26×103＝0℃-（-15℃）-15℃T＝6233s8-0-）20.0×1＊22.医学知识告诉我们：人体组织的温度等于、高于48℃的时间不能超过10s，否则该组织内的细胞就会死亡。今有一劳动保护部门需要获得这样的资料，即人体表面接触到60，70，80，90，100℃的热表面后，皮肤下烧伤深度随时间而变化的情况。试利用非稳态导热理论作出上述烧伤深度随时间变化的曲线。人体组织可看成是各向同性材料，人体组织的导热系数入＝0.635W/（m·K），热扩散率a＝15.3×10-8m2/s，比热容c＝4174J/（kg·K），密度p＝992kg/m3。计算的最大时间为5min，为简化分析，这里可假定一接触到热表面，人体表面温度就上升到了热表面的温度。【解】该题目为第一类边界条件下半无限大物体的非稳态导热42一44/245H田56l令K/s1770C84％□117：30P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:4.23Size:188.×传热学习题集和答案详……第4章“非稳态导热”习题解答问题。家以面苹山投华山中0更亩（求解方法可参考杨世铭主编，《传热学》第4版，高等教育出版社）容出的人体初温to＝37℃，t＝48℃，烧伤深度即为r＝10s到达的距离。·m）W武效系燕面副0t-t＝erfx48-t0oto-tw2a（T-10）37-t0E0＝T/min烧伤深度/mm1234560/0.50162.774.125.125.956.6870/0.68423.785.616.988.129.111280/0.80364.466.598.209.5310.7190/0.89154.937.319.0910.5711.88100/0.96005.317.889.7911.3912.790P109n2d＊23.俗语说：“冰冻三尺，非一日之寒”。试根据下列数据计算冬天冰冻三尺需几日之寒。设土壤原来温度为4℃，受寒流影响，土壤表面突然下降到-10℃，土壤物性：A＝0.6W/（m·K），a＝0.194×10-6m2/s，且入和a不随冰冻变化。【解】本题属第一类边界条件下的半无限大物体的非稳态导热问题。m800＝9，（·8）LE810t-twerf0-（-10）＝0.71430oto-tw2aT4-（-10）08-9580＝得：x＝0.755002√aT-85.0由题意x＝1m，所以：8-80T＝x2×0.755a＝1（0.194×10-6）s2×0.755＝2.26×10s＝26.17d—43—45/245175H田56l令K/s0C83％□117：30P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.36Size:188×传热学习题集和答案详……客腾传热学习题解答章＊24.在温度为250℃的烘箱中烤山芋。设山芋可以看成直径为5cm的球体，初始温度为20℃，已知山芋的导热系数入＝0.648W/（m·K），热扩散率a＝15.7×10-8m2/s，比热容c＝4174J/（kg·K），密度p＝988kg/m3。试估算烘烤20min后山芋的温度。取表面传热系数为20W/（m2·K）。_hR_20×0.025A【解】Bi＝0.7716入0.648Fo＝T-15.7×10-8x1200＝0.30144R20.025im新由拟合公式计算：（参考杨世铭主编，《传热学》第4版，高等教育出版社）812SES020000.2779、8007B1＝（0.0988＋-1/2＝1.4761Bip200808008A＝1.0003＋0.9858（1-e-03191Bi）＝1.21545（0-＝Ae-BFo＝1.21545e-L47612×03014＝0.63000m＝0.6300＝0.63×（20-250）℃＝-144.9℃tm＝0m＋t1＝-144.9℃＋250℃＝105.1℃＊25.初始温度为28℃，直径为80mm的橘子放在冰箱里，冰箱中空气的温度为3℃，空气与橘子间表面传热系数为8W/（m㎡·K）。试计算橘子中心温度降至8℃所需的时间。已知桔子的导热系数入＝0.599W/（m·K），热扩散率a＝14.3×10-8m2/s，比热容c＝4183J/（kg·K），密度p＝998kg/m3。①用诺谟图求解：Bi_hR_8×0.04＝0.53421＝1.872入0.599Bi0mtm-t8-3＝0.20oto-t128-3:，三意由查诺谟图得：e1.0）Fo＝T＝1.1→TFoR21.1×0.042＝12308s＝3.42hR2a14.3×10-844-46/2450HD56，l令243K/s0C83％□17：30P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:2.99Size:171.×传热学习题集和答案详……第4章“非稳态导热”习题解答②用拟合公式求解：（参考杨世铭主编，《传热学》第4版，高等教育出版社）902＝aNU（0-0T）x08F×1＝6m-1/2B1＝10.0988＋.277.90.27791＝（0.0988＝1.271Bi0.53421X2.0＝6A＝1.0003＋0.9858（1-e-0.391）＝1.1548001＝Ae-BPo＝1.1548e-（1271）20＝8-3＝0.2lan1成①0％8-3mxm长面①解得：nIxmIxmI进Fo＝＝1.085→T＝FoR21.085×0.042R2Q14.3×10-8＝12140s＝3.37h＊26.在太阳能集热器中采用直径为100mm的鹅卵石作为贮存热量的媒介，其初始温度为20℃。从太阳能集热器中引来70℃的热空气吹过的鹅卵石，空气与鹅卵石之间的表面传热系数为25W/（m2·K）。试问3h后鹅卵石的中心温度为多少？每千克鹅卵石的贮热量是多少？已知鹅卵石的导热系数入＝2.2W/（m·K），热扩散率a＝11.3×10-7m2/s，比热容c＝780J/（kg·K），密度p＝2500kg/m3。【解】本题属直径为100mm的球形物体的非稳态导热问题，先判断Bi数，BihR_25×0.05＝0.568不满足集总参数法。入2.2Fo＝T＝11.3×10-7×3×36002c＝4.882nieR2（50×10-3）288拟合公式：（参考杨世铭主编，《传热学》第4版，高等教育出版社）的塑平大钢的B1＝（0.0988＋2m9）＝（0.0988＋0.27791-120.568＝1.30480002AA＝1.0003＋0.9858（1-e-0.3191B）＝1.1637的＝Ae-o＝1.1637e1301242＝2.89x10-400沃前m班个一己式即：tm＝t＋2.89×10-（to-t）Rd＝70℃＋2.89×104（20-70）℃＝69.986℃—45—47/245口H田56l令K/s243⊙0C83％□17：30P:0/1dX:0.0dY:1.0Xv:0.0Yv:0.058Prs:1.64Size:171.×传热学习题集和答案详……公传热学习题解答章上最由于温度已基本与流体温度相等，则每千克鹅卵石的贮热量为：Q＝-mc0o＝1×780×（70-20）kJ/kg＝39kJ/kg（出育27.某种耐火砖体的导热系数为入＝1.12W/（m·K），热扩散率a＝0.5×10-6m2/s，初始温度为40℃，经与650℃的高温气体接触100h后，求下列3种不同砖体形状情况下的温度：00①厚度为1m的无限大平壁的中心温度；三0②截面为1m×1m方形柱体的中心温度；0③1mx1m×1m立方体的中心温度，其中一壁面绝热。上述三种情况下，壁面与高温气体间的复合换热表面传热系数均为80W/（m2·K）。采中性时空【解】①Bi＝h680×0.5入1.12＝35.70氏边盛银其.（:m）WFoT0.5×10-6×100×3600820.52＝0.72＞0.2写（Bi）解方程：tanBB＝B1＝1.528185＝00m2sinBD0分青本件0BsinB，cosBiexp（-BiFo）2sin1.5281.528＋sin1.528cos1.528exp（-1.5282×0.72）＝0.2368x62出t＝0.2368（40-650）℃＋650℃＝505.6℃②方形柱体可以看成2个厚度为0.5m的无限大平壁的交集；由①的计算结果得：＋88000＋88000＝80m柱三tm柱-65000＝（0.2368）2＝40-650＝0.056100tm＝0.0561（40-650）℃＋650℃＝615.8℃③本问题属于三维非稳态导热问题，立方体可看成是②所计算的方形柱体与一个厚度2m的无限大平壁的交集：喝Bi＝h680×1＝71.43入1.12（05＝05）01x8.5＋0＝—46—48/245H田56l令K/s112◎0C83％□117：30P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.16Size:171.×传热学习题集和答案详……第4章“非稳态导热”习题解答Fo＝aT0.5×10-6×100×3600＝0.1820，0＝8821Fo接近0.2，近似视为正规热状况阶段计算。0＋010.1＝1Bi＝71.43时，B1＝1.5491，x＝6/2处的相对过余温度：008/22sinBexp（-BFo）cos＝0.59070oB:＋sinB:cosB立方体中心温度：01x010，e-）zsT00.1＝0＝02＝0.0561×0.5907＝0.03314000o00tm＝0.03314（40-650）℃＋650℃＝629.8℃＊28.一易拉罐饮料从30℃的室温中移入5℃的冰箱冷藏室中冷却。假设罐中饮料的自然对流可以忽略，罐的直径为50mm，高120mm，其外表面与冷藏室环境的表面传热系数为10W/（m2·K），罐壳的热阻可以忽略不计。已知饮料的导热系数入＝0.599W/（m·K），热扩散率a＝14.3×10-m2/s，比热容c＝4183J/（kg·K），密度p＝998kgm，试计算为把饮料冷却到10℃所需的时间。日时小【解】本题属于二维非稳态导热问题，可采用相应的无限长圆柱体R＝25mm和无限大平板6＝60mm的乘积求解。回.袭时直hR_10×0.025对无限长圆柱Bi柱＝入＝＝0.41740.599由拟合公式：（参考杨世铭主编《传热学》第4版，高等教育出版社）0.4349-1/2B1＝（0.17＋0.4349（0.17＋＝0.9084Bi0.4174A＝1.0042＋0.5877（1-e-0.4038B）＝1.0954-＝Aexp（-BFO）＝1.0954exp（-0.9084214.3×10-8T0.0252＝1.0954exp（-1.888×10-4）人式年面集h610×0.06对于无限大平板：Bi板＝入0.599＝1.0017【147—49/245HD56l令241K/s0C83％□17：30P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.41Size:171.×传热学习题集和答案详……老神（传热学习题解答幸＋帮0.9188-1/2020B1＝（0.4022＋Bi＝0.8706A＝1.0101＋0.2575（1-e-04271）＝1.0997..0o0板＝Aexp（1-BFo）戴S8＝x.OC.1＝1日。A.I＝009020014.3×10-8＝1.0997exp-0.87062×0.062盛中本式＝1.0997exp（-3.0107×10-5）1800.0＝0020×1820-0＝09000n000-0608.050＝3020＋（020-02）A10.0＝1中室元1.0954exp（-1.888×107）×对弱良一8专1.0997exp（-0.3011×10r）.nO1＝1.2046exp（-2.1891×10-4）装的即t0--30-5＝5＝1.2046exp（-2.1891×10-r）tm-t_10-5_1解得e＝8202s＝2.278h29.材料相同、初温相同且满足集总参数法条件的金属薄板，细圆柱体和小球置于同一介质中加热，若薄板厚度与细圆柱体直径和小球直径相等，问当它们被加热到相同温度时所需时间之比。BmS＝8本hA0001【解】旦＝exp（-vQ2.0出由题意知：《学井》主爵进）：公合处由A版板柱00A＋T1.0＝V：888T板：T柱T球A板A柱A球＝6:3:2246C0030.一初始温度为t的固体，被置于室温为t的房间中。物体表面的发射率为，表面与空气间的表面传热系数为h。物体的体积为V，参与换热的面积为A，比热容和密度分别为c及p。物体的内热阻可略而不计，试列出物体温度随时间变化的微分方程式。【解】该物体在冷却或加热过程中，与周围流体间存在对流换—48—50/245H56，l令241K/s⊙C83％□17：30P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.49Size:179×传热学习题集和答案详……第4章“非稳态导热”习题解答热，与周围环境间存在辐射换热。设环境温度与流体温度相等，则单位时间内对流换热量更，辐射换热量中，和内能增量。可分别表示为：。＝hA（T-T）隔式参总录用采①，＝eAon（T4-T↑）中。＝pcVar29010dt00008190＝s-008由热平衡方程：一中。＝中。＋nim008＝2002＝注意：当物体被冷却时，。＞0，更＞0，但aT/0r＜0，故。＜0；当物体被加热时，更。＜0，更，＜0，但aT/0r＞0，故。＞0。这就是热平衡方程等式左边加上“-”的原因。0Ik00武点致的代入热平衡方程，得：回盛战味，（·2）八09＝阿-pev＝hA（T-T，）（T-T）亦，包初始条件：r＝0，T＝to＋273K31.一球形热电偶接点，设计时要求该接点与流体接触后在1s内能使其过余温度迅速下降至初始过余温度的5％。设该接点与流体间的表面传热系数为57W/（m2·K），试计算球形接点的最大允许半径。已知接点材料的物性：p＝8000kg/m3，c＝418J/（kg·K），入＝52W/（m·K）。【解】假定该题目满足集总参数法求解条件，则：（-）＝157×3x11＝0.05008000×418×R解得：R＝1.707×10-5m＝0.01707mm验算：Bi＝hR-57x1.707×10-3＝1.87x10-5＜0.1入52：好符合集总参数法求解要求。32.直径为12mm，初始温度为900℃的钢球，突然被放置于温度为25℃，表面传热系数为40W/（m2·K）的空气中冷却。已知钢球的物性如下：入＝40W/（m·K），p＝7800kg/m3，c＝600J/（kg·K）—4951/245H56，l令253K/s0C83％□17：30P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.15Size:188×传热学习题集和答案详……。传热学习题解答试确定钢球中心温度被冷却到120℃所需的时间。面不围固已、【解】Bi＝hR40×6×10-3＝6×10-3＜0.1入40:民可采用集总参数法求解：T）A＝重旦＝expha00pcv得：T）3＝120-2540×3900-25＝exp7800×600×6×10-3T＋＝一衡平由T＝520s＝8.66min33.一种火焰报警器采用低熔点的金属丝作为传感元件，当该导线受火焰或高温烟气的作用而熔断时，报警系统即被触发。报警系统导线的熔点为500℃，入＝210W/（m·K），p＝7200kg/m3，c＝420J/（kg·K），初始温度为25℃。问当它突然受到650℃烟气加热后，为在1min内发出报警信号，导线直径应限在多大以下？设复合换热的表面传热系数为20W/（m2·K）。【解】金属丝可视为圆柱体，设Bi＜0.1，满足集总参数法求解的条件，则：00＝25℃-650℃＝-625℃0＝500℃-650℃＝-150℃＝大，（·0＝00（-（·m）总果品目宝到【】＝c0.09＝-4hrAx81000-4x20x60dmpcln（0/00）-7200x420x1n（150/625）＝1.11×103m01x0.校核：Bi＝hR＝20×1.11×10-3/（2×210）＝0.053＜0.1，满足计下N算条件。婚然炎，P00式，nmCi比直粒34.一热电偶的pcV/A＝2.094kJ/（m2·K），初始温度为20℃，将其置于320℃的气流中。试计算在气流与热电偶之间的表面传热系-50-52/245口H田56l令K/s2530C83％□17：30P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:4.65Size:188.×传热学习题集和答案详……第4章“非稳态导热”习题解答数为58W/（m㎡·K）及116W/（m2·K）的两种情形下，热电偶的时间常数，并画出两种情形下热电偶读数的过余温度随时间变化的曲线。【解】时间常数T。＝pcVhA间，30奥空即近h1＝58W/（m㎡·K）时，Td＝2094/58s＝36.1sh2＝116W/（m2·K）时，2＝2094/116s＝18.05s01中00＝ex（-2）＝exp36.1所雄太的骨利人面02盛式然带王由，出则联00＝exp-2a＝exp18.05当阳面素断景水，中口人家要无量纲过余温度随时间的变化曲线如下图：时不感断果量当的所水出中人0感萌飞面001.00008＝0:械1代外都大小本面验【h＝E00.0）0入35.有一小型浸没式热水器，体积为1.6×10-3m3，外表面积为3.2×10-3m2。热水器由p＝8940kg/m3，A＝260W/（m·K）和c＝420J/（kg·K）的金属制成，消耗功率40W。热水器浸在水中，所以不会超过熔点538℃。由于操作人员疏忽，热水器未浸在水中而是在空气中就接通电源。假设空气与热水器间的表面传热系数恒为11.4W/（m2·K），试计算热水器达到熔点所需的时间＝K品日。了本一伏【解】热水器定型尺寸：1.6×10-3高的位m1.0千A3.2×103m＝5×10-3mL＝天11.4民【】Bi＝＝260×0.005＝2.19×10＜0.1本题为有内热源的集总参数问题，其解为：q2s＝1更t-tohA1-e-/re）＋（to-tn）e-/r1.0-9x00＝000EXASX-01841.0V-51—53/245口H田56l令K/s74.70C83％17:30P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.66Size:188！×传热学习题集和答案详……［传热学习题解答幸料11.4×3.2x103（-mW82面的3TepcV8940×420×1.6×10-5怀两出画我，喜＝6.072×10-4s-100假设初温和空气温度均为20℃，则：E＝884005＝11--6.02×10-48＝，538-20＝0.211.4×3.2×10-3n）Awal＝T＝1053s＝17.55min36.体温计的水银泡长1cm，直径为7mm。体温计自酒精溶液中取出时，由于酒精蒸发，体温计水银泡维持18℃。护士将体温计插入病人口中，水银泡表面的当量表面传热系数h＝100W/（m2·K）。如果测温误差要求不超过0.2℃，求体温计插入病人口中后，至少要多长时间才能将体温计从体温为40℃的病人口中取出。水银泡的当量物性值为：p＝8000kg/m3，c＝430J/（kg·K）。【解】水银泡体积小，入大，可以用集总参数法简化分析。L＝VT（0.0035）2×0.01m＝1.4894×10-3mAT（0.0035）2＋0.007×0.01周一，OTh.1试），器烘货小，己8＝exp，m018＝.0由器衣。m01xS.80.2100闻金（牙·8）NU18-40exp8000×430×1.4894×10-3由。38E额场T＝241s＝4min百由37.在冬季，某个地方一天内大地表面最高温度为8℃，最低温度为-4℃。已知土壤的入＝0.6W/（m·K），a＝0.194×10-6m2/sc试问地表下0.1m处的最高、最低温度为多少？达到最高温度的时间滞后为多少？m01义＝m【解】该题目为周期性非稳态导热问题。由题意知，该地面当天温度波振幅A＝±6℃。地表下0.1m处温度波振幅为：A＝A.01-x回签总隶的感内火本＝6xexp-0.1x3.14℃W0.194×106×24×3600—52—54/245口74.7H田56，l令K/s0C83％□117：30P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.80Size:188.×传热学习题集和答案详……第4章“非稳态导热”习题解答＝1.53℃tmaxtmin8-4＝2℃翰蟹区“2媛2可燕兽章0.1m处最高温度：t＝tm＋Axi＝2℃＋1.53℃＝3.53℃0.1m处最低温度：后1to.＝tm-A21＝2C-1.53℃＝0.47℃滞后时间：过更的行土间空，间团：联思本基【】宝一箱枣，潜外来合果陌5＝2的⊥点照音，漫公食书装料宝124×3600所水调：返＝20。0.194×10x3.140.1＝18830s＝5.23h思思本基朗氏娟立衡平阳：里割，元端小大阳中食端北本小娟用【客】女量内味量整内己量卡由，量术示女周出世宝式点芽系关平量画菩司由面，廊泵阳势告公书式，避胖食十朗式蜡离雅县赋出替升量小音田告眠冈生的试赠己式代【容】美，翼阳司气替升客点离谷鼠咨而，量小钢天替县式辯，泡，楚函想回空画团县念懋中料爵王神香长出些飘工来章本阳书杀界的。5肤态非亦发等食人升0＝p用，中代态影一【容】面，恩衡平量干基前，三泰早平大，中公将读的干基县管始隆宝一香最蛋式姓升永外数赛高己安当面查合不好则耐长因否最蛇刘出小？5355/245口HD56l令279K/s⊙C83％□117：30P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.22Size:196！×传热学习题集和答案详……第5章“导热问题数值解法”习题解答2＝P1.试简要说明对导热问题进行有限差分数值计算的基本思想与步骤。30＝021【答】基本思想：把在时间、空间上连续的温度场用有限个离散点温度的集合来代替，通过求解按一定方法建立起来的关于这些点温度值的代数方程，获得各离散点上的温度值。步骤：按所求问题的几何形状、求解精度和稳定性条件划分差分网络；按物理条件和边界条件建立各节点差分方程，构成差分代数方程组；求解。808881＝2.试说明用热平衡法对节点建立温度离散方程的基本思想。【答】用有限小元体代替微分分析中的无限小微元体，用傅里叶定律写出与周边元体的导热量，由净导热量与内热源量和内能增量之间的能量平衡关系得到节点方程。3.推导导热微分方程的步骤和过程与用热平衡法建立节点温度离散方程的过程十分相似，为什么前者得到的是精确描写，而由后者解出的却是近似解？【答】差分方程与微分方程的主要区别是前者用有限小量代替了后者的无限小量，前者用各离散点参数代替了后者的连续参数。实际上物体中的物理参数是时间和空间的连续函数，所以，微分方程是精确解，而差分方程是近似解。4.对绝热边界条件的数值处理本章采用了哪些方法？试分析比较之。【答】在稳态导热分析中，用q＝0代入方程式。在非稳态导热分析中，对无限大平板导热t＝，前者是基于热量平衡原理，而后者是基于温度分布的对称性原理。5.用高斯-赛德尔迭代法求解代数方程时是否一定可以得到收敛的解？不能得出收敛的解时是否因为初场的假设不合适而造成？-54—56/245口HD56l令205K/s0083％□17：30P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.20Size:171.×传热学习题集和答案详……第5章“导热问题数值解法”习题解答二【答】高斯赛德尔迭代法求解代数方程时不一定能得到收敛的解，其原因不是因为初场的假设不合适，而是由于迭代方式不合适。华（i）6.有人对一阶导数提出了以下表示式：面黄庭出不菜（）-3＋5t1（i）-tn＋2（林蓝）元E上记图0axn丙出24x2您能否判断这一表达式是否正确，为什么？at（）（【答】这一表达式不正确。的实质是求解函数一阶导数ax的三点公式。由泰勒级数可导得一阶导数的近似公式：t＇（x）tn＋1-tn△x△x2＂（x）tn＋2-ta＋1tn＋1-tn△x△xtn＋2-2tn＋1＋tn）At＂（x）＝△x（△x）2代入上式得：t＇（x）≈-3tn＋4tn＋1-tn＋22Ax＋（一）＋正确的表达式应是：L（4）-3t＋421-2BAaxnj2△x7.什么是显式格式？什么是显式格式计算中的稳定性问题？代定【答】心在非稳态导热的差分分析中，取温度对时间的向前差分，使后一时刻的温度分布完全取决于前一时刻的温度分布，而不必联立方程求解。这样的差分格式称为显式。在显式计算中，时间步长和空间步长的选择会影响求解过程的稳定性，选择得不适当会使温度产生震荡，而不收敛于某一数值，这是不符现实的。8.非稳态导热采用显式格式计算时会出现不稳定性，试述不稳定性的物理含义。如何防止这种不稳定性？【答】在显式格式离散方程中，后一时刻的温度取决于前一时刻的温度，同一节点温度前的系数有出现负值的可能性。如果出现负值，就意味着该点温度在前一时刻温度越高，则后一时刻温度将越低，-55—57/245才K口H田56l令K/s2050C83％□117：30P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.26Size:179.×传热学习题集和答案详……等除”传热学习题解答”章己甚至会出现比周围节点温度还要低的现象，这违背了热力学第二定律。为防止这种导致数值计算不稳定性的现象发生，要求空间网格△x和时间网格△的选取必须满足一定的条件，从而使同一节点的离散系数不出现负值。9.如图5.13所示（见教材）的圆截面直肋的一维稳态、无内热源、常物性导热问题。已知圆截面直径为d，试分别列出内节点m和端部节点M的离散方程式。大【解】对节点m列热平衡式：（圆截面积A。d，周长U-Td）蝶山。左公放三图tm-1-tA-△xtm＋1-tm＋hUAx（t-tm）＝0＋AA-△x4h（Ax）2tm-1＋tm＋1＋入d1即tm＝一4h（△x）2＋2Ad对节点M有：发上人升1-＋4.（-）＋h02（-）＝0A-△x＝（）2h（Ax）2hAxtM-1＋入d入中即tM＝2h△x2，hAxASXAd入易士10.试将直角坐标中的常物性、无内热源的二维非稳态导热微分方程化为显式差分格式，并指出其稳定性（条件）（△x≠△y）。一司空【解】微分方程：为易。发显为滑代羊复。轴靠半Ot22氧，家意的导兔郎滑会阳升玉国axay宝差分方程（显式）：出会享发器为显雨来态业81＋-21＋-2（i）a＋△T（Ax）2中式蜡商大（4y）2【＝F（1n＋1）＋F（-1＋＋1）＋［1-2（F＋Fo］，高更感候如一前更点尚音意，56一58/245才K0HD56，l令187K/s⊙083％117：30P:1/1X:337.6Y:910.5Xv:-8.234Yv:-2.161Prs:3.90Size:188.×传热学习题集和答案详……第5章“导热问题数值解法”习题解答a△TFa△T（△x）2（4y）2稳定性条件为：Fa＋F≤2°111.在图5.14所示（见教材）的有内热源的二维导热区域中，一个界面绝热，一个界面等温（包括节点4），其余两个界面与温度为t的流体对流换热，h均匀，内热源强度为更。试列出节点1，2，5，6，9，10的离散方程式。【解】0＋i8S＋1＋1＋a3S节点1：＋ts-t1△x△x24△vyD-24yh（-）＝0节点2：＋＋1t-2△x＋NAx2t3t2△y.1N△y112＋入Ax2＋24x4y＝0:原节点5：t1-ts△x，to-ts△x4y2＋y2＋-△y＋2Ar△y-Ayh（5-（）＝0＋1）节点6：:01背-x＋-y＋A5-△y＋△x△y＝0△y50-t6△x＋AxxA＋3＋e＋＋a小节点9：一＋（to-t）＝0△y21△x△y-h（台士）节点10：t6-0x＋tg-t1oAyt-tioAy1＋入△x2S△x＋2T2△xAy①-h△x（t1o-t）△y＝0当△x＝△y时，以上各式简化成下列离散方程式：节点1：，的蜡贷县果其，升断浓谢过高:题式外【】—5759/245H田56l令187K/s⊙083％117：30P:0/1dX:-269.6dY:-17.5Xv:-10.263yv:-0.580Prs:1.73Size:139.×传热学习题集和答案详……衣”传热学习题解答中ts＋t2＋（）（A）t，＝2＋Bi节点2：一阳山育（体樊贝）衣1。图。11＋＋t＋Ay更点群）感面个一装界＝40，节点5：先式蜡离的2t＋ti＋tg＋2Bi4＋△y2【】入ts＝:点2（2＋Bi）节点6：一3）△x5人＋-0＝-（＋0＋5＋＋A21节点9：＝L＋5品点tg＝2（1＋Bin）人＋小节点10：00＝△＋7△人＋＋一YA公2t6＋t＋tg＋2Bigtr＋Ay2中入:点t10＝2（2＋Bi）-D么A式中：BiA＝hAySAA:01点12.试用数值计算证实，对方程组0-rx1＋x2-2x3＝14x1＋2x2＋x3＝30＝发2x1＋2x2＋x3＝5L＝L用高斯赛德尔迭代法求解，其结果是发散的，并分析其原因。【解】迭代方程：-58-61/245H田56，l令187K/s⊙0C83％□17：30P:0/1dX:-346.0dY:-13.0Xv:-9.855Yv:-0.370Prs:0.96Size:155.×传热学习题集和答案详.热问题数值解法”习题解答1-x2＋2x31（x）＋3-x1-x3）△）＋（、，微5-2（x1＋x2）yA）x△＋，234＝4:519.52.5送17.751.5＋1021.5＝、-3.255.755140800-11公品m7.50＋8TQ0＝阵不满足主对角线占优条件。润，肋根温度为to，流体温度为t表面传。将它均分成4个节点（见教材图5.15），件（h同侧面）的两种情况列出节点2，5mm，6＝10mm，h＝50W/（m2·K），，t＝20℃，计算节点2，3，4的温度（对0＝x:式果节点2，3，4的离散方程：杰内本林3-2）8＋2△xh（t-t2）＝0△x】式点苹界发一9＋t3）＋2h（Ax）2t8＋h（△x）2变器，应然墙2＋t4）＋2h（Ax）2t［8＋h（△x）2的中面处塑厨盛00的回女已面h△x（t1-t4）＝0，m10—59一Y62/245H田56l令265K/s⊙083％117：30P:0/1dX:-210.1dY:-8.6Xv:-8.428Yv:-0.354Prs:1.54Size:155.×传热学习题集和答案详……第5章“导热问题数值解法”习题解答1【答】由于该汽包周长及长度都远大于汽包壁的厚度，该问题可视为一无限大平壁的非稳态导热问题。又因为汽包内表面与水之间对流换热十分强烈，即五一→∞，所以汽包内表面可视为第一类边界条件，外表面为绝热。。（·山）八W三效面泰将该汽包壁等分为11段，取时间步长△r＝5s，其各节点离散方程如下：民第一类边界：4P＋1）-P＋1.3A＝1＋1.31to800＝000s-012内部节点：tP＋1）＝Fo（t（P1＋tP1）＋（1-2Fo）tP），m＝1，2，…，10绝热边界：＋1）＝o0.0x.8x△Fo＝a4T_9.98×10-6×5，8:（高内）＝0.499△x27（0.11/11）21-2F0＝1-2×0.499＝0.002＞0满足稳定性条件。编程计算后截取相关时刻温度分布如下：T/min051015202530节点0100106.5113119.5126132.51391100105.27111.29117.53123.89131.12136.782100104.23109.78115.77121.99128.34134.763100103.37108.47114.21120.30127.38132.994100102.66107.34112.85118.82125.03131.385100102.09106.38111.69117.54123.69130.056100101.63105.59110.71116.46122.56128.857100101.28104.95109.92115.59121.64127.968100101.02104.46109.31114.91120.92127.169100100.85104.12108.87114.43120.41126.7110100100.74103.92108.61114.13120.10126.3211100100.71103.85108.52114.04120.00126.2910min时界面中的最大温差：（113-103.85）℃＝9.15℃20min时界面中的最大温差：（126-114.04）℃＝11.96℃0三：部长30min时界面中的最大温差：（139-126.29）℃＝12.71℃仪山-61—63/245口H田56l令265K/s⊙C83％□17：30P:0/1dX:-285.8dY:11.3Xv:-7.875Yv:0.295Prs:0.85Size:147.×传热学习题集和答案详.法”习题解答大于汽包壁的厚度，该问题可16.有一砖墙又因为汽包内表面与水之间J/（m3·K），室内温内表面可视为第一类边界条稳定状态，且内表01-10℃，外墙表面长△r＝5s，其各节点离散方下降0.1℃是可感多少时间内墙才感46P＋L3国【）【答】该问题12果第三类边界条件。（1-2Fo）tP，m＝1，2，…，10m，则：，8：（内）界式左边界（内墙满足稳定性条件。右边界（外墙如下：为满足稳定性202530因为Bi1＜Bi2乡126132.513953123.89131.12136.78取时间步长△121.99128.34134.76Fo＝aAT120.30127.38132.99（Ax）po118.82125.03131.38即满足稳定性69117.54123.69130.05内墙：4P＋1）＝1116.46122.56128.85内部节点：t92115.59121.64127.96外墙：8＋1）＝31114.91120.92127，16将F。，Bi，Bi2＞114.43120.41126.71114.13120.10126.32内墙：tS＋1）＝（52114.04120.00126.29内部节点：t9.15℃2，…，91.96℃0＝5:谢树外墙：8＋1）＝（2.71由该墙初始处64/245H田56l令381K/s⊙083％117：30P:0/1dX:-335.3dY:1.5Xv:-10.588v:-0.015Prs:1.33Size:163.×传热学习题集和答案详……酿区传热学习题解答章菜6.有一砖墙厚8＝0.3m，A＝0.85W/（m·K），pc＝1.05×10°3·K），室内温度ta＝20℃，h1＝6W/（m㎡·K）。起初该墙处于状态，且内表面温度为15℃。后寒潮入侵，室外温度下降为t2＝℃，外墙表面传热系数h，＝35W/（m2·K）。如果认为内墙温度0.1℃是可感到外界温度起变化的一个定量判据，问寒潮入侵后时间内墙才感知到？答】该问题可视为一无限大平壁的非稳态导热问题，两侧均为类边界条件。将该砖墙沿壁厚分成10段，△x＝6/10＝0.035.1＝m405h1Ax6×0.03左边界（内墙）：Bi1＝入0.85＝0.211765右边界（外墙）：Bi2＝h2Ax35×0.03入折0＜0.85＝1.23536-11为满足稳定性条件Fo≤Bi＋21因为Bi1＜Bi2，即Fo≤＝0.223684Bi2＋22×1.2353＋2取时间步长△r＝6min＝240s，则：0t001aArA△T0.85x240＝0.215873＜0.223684（△x）2pc（4x）21.05×10×0.032即满足稳定性条件。则各节点离散方程如下：001内墙：tP＋）＝2FotP）＋［1-2Fo（1＋Bi1）］tP）＋2FoBi，t内部节点：tP＋1）＝Fo（t1＋t1）＋（1-2Fo）tP，m＝1，2，…，9外墙：＋）＝2）＋［1-2Fo（1＋Bi2）］t＋2FoBi2t2将F。，Bi1，Bi2的数值代入后，各节点离散方程如下：内墙：6＋1）＝0.431746t）＋0.476825326＋1.828574内部节点：tP＋1）＝0.215873（t1＋tP1）＋0.568254tP，m＝1，，9OE外墙：t＋1）＝0.431746tP＋0.034918t-5.3336mine05由该墙初始处于稳定状态可得：a1-E1）大中面mOE一62—65/245H四56l令381K/s◎0C83％□117：30P:0/1dX:-228.6dY:22.3Xv:-8.079Yv:0.677Prs:1.03Size:147.×传热学习题集和答案详……赖尽“传热学习题解答“章【解】本题可视为一维无限大平壁的非稳态导热问题，将冷柜门厚度由内向外均分为8段，即△x＝0.08/0.8m＝0.01m，取△r＝30s补充求解条件：a＝4.5×10-7m2/s9°由题意知，冷柜门内侧为第一类边界条件，其节点方程为：t8P＋1）＝8P）-18×4/3600＝tP）-18×30/3600:由801＝t）-0.15℃内部节点方程：9t＋1）＝Fo（t＋t）＋（1-2Fo）（P）（n＝1，2，…，7）9采用热平衡法可列出冷柜门外侧（节点8）的离散方程：8）-tgP）（P）、144入一△x＋1.55（t-）＋eo（T-（T）4）Ax-＋1）-（P）10.01a5.0a5）Epc2△Ter815.0整理后得：0.8.00520.80（P＋1）（P）＝201-）0.014809（20-°）4＋0.0459520.3612.934-1917101Fo＝aAT＝4.5×10-7×30＝0.135到外修要11.0（Ax）3（0.05/8）2代入Fo，入的数值后，各节点方程为：开启良＋1）＝6）-0.15℃。柜tP＋1）＝0.135（t2＋tB）＋0.73tPn＝1，2，…，7。冰＋1）＝P＋0.27（P-4）＋0.19992（20-4P）5＋及与面0.6123612.93-1编程计算得到2h内的温度场数据，冷量损失为：8＝Q＝入A△Tt（P）-toP）8动后司时＝0.02×1.2×1.2×30/0.01（tP）-t8P）—64—66/245H田56l令381K/s⊙0C83％□17：30P:0/1dX:-243.1dY:10.3Xv:-9.229Yv:0.429Prs:1.46Size:139.×传热学习题集和答案详……第5章“导热问题数值解法”习题解答，将冷柜门＝89216.5J△T＝30s。18.一厚0.2m，温度为80℃的无限大平壁，突然放8境中对称加热，壁面与环境的表面传热系数为1163W为：料的导热系数为50W/（m·K），热扩散率为1.39×10:由数值解法确定15min和30min时平壁内的温度分布。m【解】/由于对称受热，取半平板划分10段网格进中心节点，11为表面节点，节点方程如下：：来，7）中心节点为绝热边界：t＋＝908-08）2蓝采内部节点：tP＋1）＝Fo（tP1＋tB1）＋（1-2Fo）tP，））图壁面：P＋）＝2Fot8＋［1-2Fo（1＋Bi）］tP＋2Fol根据稳定性条件选取时间网格，编程计算（略）。式19.建筑物采暖的一种方式是在房间地板下设置热图5.17所示（见教材）。设地板下混凝土层的一侧绝热t2＝30℃。热空气通道截面尺寸为150mm×150mm，中对称布置，通道壁温保持为t1＝80℃。试计算单位长的传热量，并从计算结果中整理出此种情形下形状因子0E88.0308.1801823040121克3内部:F88.0S0E.，008，01.E88式6补Q秋量的器1务，琳酒89长110111213民，中其【解】这是一个二维稳态导热问题。由于空气通80对称布置，选取如下图所示的传热单元进行求解，其中节n＝1，m＝1～5为恒壁温30℃；—65—67/245H田56l令377K/s⊙0C83％□117：30P:0/1dX:-210.5dY:-7.4Xv:-9.039Yv:-0.283Prs:1.80Size:139.×传热学习题集和答案详……公区”传热学习题解答m＝1，n＝2～12为绝热边界；10108＝n＝13，m＝1～5为绝热边界；08林（m＝5，n＝2，12为绝热边界；面素液已面望，中意m＝1，n＝2～12为绝热边界；燕，（·m）W02式菜号的m＝3，n＝3～11为恒壁温80℃；mim0E麻nim己！宝面直0m＝4，5，n＝3，11为恒壁温80℃；其余为内部节点；△x＝2△y，列出各节点方程编程求解得：中＝399入。点点面长1，点芽小中由更1＝入S△t＝入S（80℃-30℃），得此种情形下形状因子S＝7.98。01、20.烟道墙内、外壁分别维持在650℃和50℃，墙体由导热系数为1.4W/（m·K）的材料砌成。）墙体尺寸及1/4角的网格划分如图5.18所示（见教材）。试确定节点1～6的温度分布及通过每米长该墙的热流量。如果内壁与温度为650℃、表面传热系数为100W/（m2·K）的流体接触，而外壁与温度与50℃、表面传热系数为25W/（m2·K）的流体接触，试重新计算温度分布和散热量。了0E＝【解】该题是一个二维稳态导热问题，△x＝△y＝0.5m。海①当烟道墙内、外壁分别维持650℃和50℃时，编程求解得节点1～6的温度分别为325.12，300.24，175.84，303.11，336.60，343.30℃通过每米长该墙的热流量为7424.7W。②当烟道墙内、外壁均为第三类边界条件时，编程求解得节点16的温度分别为333.16，306.64，186.00，310.01，346.26，353.74℃通过每米长该墙的热流量为6948.3W。中生路斯子空牛由国态多二个一点中其，求示单图图一66一68/245口田56ll令K/s377o083％17:30P:1/1X:761.2Y:53.0Xv:0.0Yv:0.0Prs:3.52Size:171.×传热学习题集和答案详……的两面，向长式回达面塑第6章量“对流换热的基本方程”习题解答界类三袭成类一：宝厨由同不同不出出161.用水和同温空气冷却物体，为什么水的表面传热系数比空气大得多？由需，量眠未味，量与发友壺扑杀界【答】水的导热系数比同温度下空气的导热系数大20多倍，其以导热方式传递热量的能力比空气强；水的比热容比空气的比热容大得多，常温下水的pc，～4180kJ/（m3·k），而空气的pcp～2kj/（m3·K）。两者相差悬殊，水以热对流方式转移热量的能力比空气大得多，因此水的表面传热系数比空气大得多。参本端，【】2.叙述理论求解表面传热系数的基本途径。【答】对于常物性流体的对流换热问题，温度场与速度场可分别独立求解，属于非耦合问题。理论分析求解表面传热系数的基本途径是：①由连续性方程和动量微分方程结合定解条件求出速度场；②已知速度场后，由能量方程结合定解条件求出温度场；③由对流换热过程微分方程式求出局部表面传热系数；④由积分方式求出平均表面传热系数。436如物性随温度变化，温度场与速度场必须联立求解，属于耦合问题。660三（3.略。4.对流换热过程微分方程式与导热过程的第三类边界条件表达式，两者有什么不同之处？长左赤的【答】对流换热过程微分方程式：U615＝h＝一at（t-t）ay）w图【】第三类边界条件表达式：11＝0（）（t｜-t）:联（林由67一Y69/245才K0中H田56令377K/s◎0C83％□117：30P:0/1dX:-274.1dY:6.4Xv:-10.078v:0.258Prs:1.49Size:155.×传热学习题集和答案详……的两面明，回式式回式婴达面塑第6章量“对流换热的基本方程”习题解答发蛋式食端壁盘奥这。量氏县中杀界女类三袭成类一：宝康由同不同不出田1.用水和同温空气冷却物体，为什么水的表面传热系数比空气大得多？由需，量联成味，量中发表书杀界【答】一水的导热系数比同温度下空气的导热系数大20多倍，其以导热方式传递热量的能力比空气强；水的比热容比空气的比热容大得多，常温下水的pc，～4180kJ/（m3·k），而空气的pc～1.2k/（m3·K）。两者相差悬殊，水以热对流方式转移热量的能力比空气大得多，因此水的表面传热系数比空气大得多。参本，回二【早］2.叙述理论求解表面传热系数的基本途径。氏团它量【答】对于常物性流体的对流换热问题，温度场与速度场可分别独立求解，属于非耦合问题。理论分析求解表面传热系数的基本途径是：①由连续性方程和动量微分方程结合定解条件求出速度场；②已知速度场后，由能量方程结合定解条件求出温度场；③由对流换热过程微分方程式求出局部表面传热系数；④由积分方式求出平均表面传热系数。436如物性随温度变化，温度场与速度场必须联立求解，属于耦合问题。0三3.略。64.对流换热过程微分方程式与导热过程的第三类边界条件表达式，两者有什么不同之处？长＆卖阳嫂函端其，式【答】对流换热过程微分方程式：65＝h，＝一at（t-t）ay第三类边界条件表达式：（部）h入（t一t）:（）先标由67一69/2450H田56l今222K/s⊙083％117：30P:0/1dX:-260.3dY:-19.2Xv:-11.24v:-0.826Prs:1.73Size:155.×传热学习题集和答案详……传热学习题解答线方向为y方向，则（）.-（）.，t＝t，可见两者的致的。但h，为局部值，在方程中是未知量；h为平均值，界条件中是已知量。对流换热过程微分方程式中，因边界条件不同而不同，由温度场确定；第三类边w.x达阳公，式中，t为已知量，t和an为未知量，仍需由温度场圆柱坐标系的二维连续性方程，假设流体为常物性不可空为益二维问题，微元体参看教材图2.5（a），取微圆环建立质己（M，-M2＋d）＋（M，一M，＋）＝0常干【】aMx，M，dr＝M，aM.＋axMdr，代入守恒方程得：出柔aM，aM，，由①dx-dr＝0出来我杀ox宝合吉or量由，夏联图M＝2mpurdr，M，＝2purdx长代由2mpr（vr）drdx＝0来立audrdx＋2mpx要器ar劐，卜变博du1a（r）＝0axrar性不可压缩牛顿型黏性流体掠过壁面的二维对流换热散函数的表达式为：仪女同不公音两，方＝2（＋21（＋加自门【容】耗散函数定义为：＝［（duduax＋Tyay1＋0w）1＋Tyay类三T对x（6.7）知：一68Y71/245349月56，ll今K/sO83％17:30P:1/1X:763.4Y:49.2Xv:0.0Yv:0.0Prs:3.43Size:171.×传热学习题集和答案详……答”传热学习题解答”章ò8.能量微分方程Dtdr0dx2与固体导热微分方程1ata2ax？ay2）两者有何区别？什么情况下能量微分方程可转化为固体导热微分方程？发人分【答】能量微分方程是在流场中取微元体根据能量守恒定律推导得出，固体导热微分方程式是在固体中取微元体根据能量守恒定律推导得出。前者考虑了热对流过程、导热过程和作用在微元体上的外力对微元体内流体所做的净功，后者仅考虑了导热过程，因此两个方程是有区别的。当流体静止时，u＝0，v＝0，此时：常5Dtatatdxatdyat＋uattoatatdTataxdTaydTaraxdy望平上山能量微分方程转化为固体导热微分方程。。氏量虑踊民量二的中坐前【］664＋66＋6x616.0614＋9666ds0066.06惠游干田式尘准，盛望平土平可.0＝A.0＝，:态，练朴不。望干退代霖食量间x，x.。O＝00＝0:团家武代06606T6:外简064x＝9606066:比式660＝18C6＊x96b70-72/245中0H田56ll令K⊙C83％□17：30P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.04Size:188×传热学习题集和答案详……传热学习题解答”章ò8.能量微分方程与固体导热微分方程atdrx2＋ata2ax？ay2）两者有何区别？什么情况下能量微分方程可转化为固体导热微分方程？昏，先生人升【答】能量微分方程是在流场中取微元体根据能量守恒定律推导得出，固体导热微分方程式是在固体中取微元体根据能量守恒定律推导得出。前者考虑了热对流过程、导热过程和作用在微元体上的外力对微元体内流体所做的净功，后者仅考虑了导热过程，因此两个方程是有区别的。当流体静止时，u＝0，v＝0，此时：DtatatdxatdyattuattatatdTataxdTaydTaraxaydT春塑平、山能量微分方程转化为固体导热微分方程。比县量二的中坐前直【果】66/4＋961616666，3/06＋966616惠园干田式尘准，望平土，壁平可0＝，.0＝，:态，朴不。望在干退际新式西，毒食食量间，x.。0＝0.0＝0：这：0＝6606T6:庆外简06496066:比式量_好4x6018C69670—72/2450。合k/s0C83％□17：30P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.81Size:188.×传热学习题集和答案详……第6章“对流换热的基本方程”习题解答露计食利Tx＝2u＝24，8du科固式群式TFTx＝ay＋x代入上式，得：＝（2（＋（8＋2）J＋［（＋）（）＋2（＝2（）＋（＋》＋2（门洁前。出早得证。7.常物性流体在两无限大平行平壁间做稳态层流运动，下平壁静止，上平壁在外力作用下做等速运动，速度为。试推导描述流体运动的动量方程。【推导】直角坐标系中的二维动量方程为：式婚量＋1Paraxay＝F-卫＋a100J0＋0201T＝（araxay/卫＋yay（＋）下平壁静止，上平壁匀速运动，在黏性力作用下拖动着流体匀速流动，可视为流动处于充分发展段。不计体积力，稳态：F＝0，F，＝0，-0，＝0；充分发展时：0＝0，＝0。所以x，y向的动量方程分别ax简化为：＋ax8＝0p＝0ay故axdx，动量方程为：dx8＝0一6971/2450083％□17：30P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:2.96Size:179！×传热学习题集和答案详……传热学习题解答取壁面法线方向为y方向，则（就）.-（）.，＝，可见两者的表达形式是一致的。但h为局部值，在方程中是未知量；h为平均值，在第三类边界条件中是已知量。对流换热过程微分方程式中，（t一t）（）因边界条件不同而不同，由温度场确定；第三类边wx界条件表达式中，t为已知量，t和（）为未知量，仍需由温度场目，05大度滚鼎吊四空确定。5.试推导圆柱坐标系的二维连续性方程，假设流体为常物性不可压缩流体。大空出的量典海发【推导】二维问题，微元体参看教材图2.5（a），取微圆环建立质量守恒方程：长回N己（M，-M＋d）＋（M，-M，＋）＝0常干【容】小其中系aM立烟式中，M＋da＝M＋dx，M，＝M，＋dr，代入守恒方程得：adr敦出永aMaM运味氏由①dx-dr＝0:过变出求书条ax合吉or式量由，合联但：嫂系M2＝2mpurdr，M，＝2mpurdx肤处青试由故氏用由④2Tmpaudrdx＋2mp（ur）drdx＝0合干闻，立美美高，外变盛卧整理得u1（vr）＝0回axrar6.以常物性不可压缩牛顿型黏性流体掠过壁面的二维对流换热为例，证明耗散函数的表达式为：投支同不公告两，发MD＝12（＋2怀【容】aydx【证明】耗散函数定义为：＝［（＋一＋au＋Twayav］世兆三T对x由教材式（6.7）知：68—70/245H四56，ll令K/0⊙0C83％□17：30P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:2.80Size:171.×传热学习题集和答案详……的两面，回试式回式婴达面塑第6章量“对流换热的基本方程”习题解答式食端壁饮量氏县中料杀界女类三袭成类一：宝过康由不而同不出出用1.用水和同温空气冷却物体，为什么水的表面传热系数比空气大得多？由需母，量联末味，量联与中发双麦杀界【答】水的导热系数比同温度下空气的导热系数大20多倍，其以导热方式传递热量的能力比空气强；水的比热容比空气的比热容大得多，常温下水的pc，～4180kJ/（m3·k），而空气的pc～1.2kJ/（m3·K）。两者相差悬殊，水以热对流方式转移热量的能力比空气大得多，因此水的表面传热系数比空气大得多。参本，回二【早］2.叙述理论求解表面传热系数的基本途径。【答】对于常物性流体的对流换热问题，温度场与速度场可分别独立求解，属于非耦合问题。理论分析求解表面传热系数的基本途径是：①由连续性方程和动量微分方程结合定解条件求出速度场；②已知速度场后，由能量方程结合定解条件求出温度场；③由对流换热过程微分方程式求出局部表面传热系数；④由积分方式求出平均表面传热系数。如物性随温度变化，温度场与速度场必须联立求解，属于耦合问题。0＝（163.略。64.对流换热过程微分方程式与导热过程的第三类边界条件表达式，两者有什么不同之处？长左赤的函，长【答】对流换热过程微分方程式：5月＝h，＝一at（t-t）ay第三类边界条件表达式：（部）h入（t一t）:（）先标由67一69/2450HD56，l令96.1K/s00C83％C□17：31P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.54Size:179.×传热学习题集和答案详……传热学习题解答界层中的速度分布和温度分布具有类似的规律。由于边界层中存在温度梯度，因此产生了热量的传递，传递的热量具体体现为热流密度q；由于同时存在速度梯度，因此产生了动量传递，传递的动量具体体现为黏性应力。温度分布与速度分布的相似性说明热量传递与动量传递具有相似性。雷诺类比适用于P＝1的流体。，内果都平7.P大的流体一般黏度比较大，而经验告诉我们黏度较大的流体对流换热一般比较微弱，但在换热准则函数关系式Nu＝f（Re，Pr）中，Pr大的流体表面传热系数反而比Pr小的流体要大，这与经验是否矛盾？请解释其原因。息成：中量【答】黏度越大时，Pr数越大，但Re数越小。由教材式（13）知：束其变其Nu＝cRe＂Prm即hl公升式，郡入（（台量h＝c（ul）＂a＂-cau/＇P-la【容】通常情况下，受迫流动换热时，n＞m。可见h与v成反比，即v越大，h越小。例如，外掠平壁层流对流换热时，Nu＝0.664Re12P13，即n＝1/2，m＝1/3，n＞m；再如，外掠平壁湍流对流换热时，类比公式为：Nu＝（0.037Re12-870）P13，仍然n＞m。8.外掠平壁层流边界层稳态流动，取无量纲坐标7＝2y√x，无量纲流函数f＝。试推导求相似解的无量纲动量方程并写出√uvx相应的边界条件。【推导】动量微分方程和相应的边界条件为：用出类箭u＋u，2u藏量公òaxdyay是y＝0:u＝0量u＝0面.待界【客】-72—74/245口96.1H田56l令K/s0C83％□17：31P:0/1dX:-0.5dY:2.5Xv:-0.027Yv:0.135Prs:3.28Size:179.×传热学习题集和答案详……第7章数“对流换热的求解方法”习题解答已型量灯代新语要代1.外掠平壁层流边界层内，为什么存在壁面法线方向（y向）的速度v？阳大更礼健面，天货为更婚一大，中（【答】y向的速度v是由于边界层不断增厚，所排挤掉的流体产生的速度。已，大受本燕增小面灵系面本的大2.在对流换热的理论分析中，边界层理论有何重要意义？雷:【答】边界层理论的主要意义在于，利用边界层的特征采用数量级分析法来简化对流换热微分方程组，使其变成更容易求解的形式，从理论上寻找出便利于求解h的途径。3.根据数量级分析，边界层连续性方程并未得到简化，为什么？【答】这充分说明y向的速度v与边界层厚度6属同一数量级的微小量。m＜m，血受，T常喝，4.解释边界层中＝0的物理意义。dy韩则小强大:发公【答】＝0说明沿壁面法线方向压强P并不发生变化，边界层ay外主流区压强变化的规律可推广应用到边界层内。5.为什么Pr＞1的流体，8＞8【答】P＞1，说明流体传递动量的能力大于传递热量的能力，因此6＞6。由积分方程解也可以证明这一点。由动量积分方程得：8。书炎界≈Pr-1。所以，Pr＞1时，8＞81。8式伦焰量【】6.为什么热量传递和动量传递具有相似性？雷诺类比适用于什么条件？66【答】通过边界层分析，得到的边界层动量微分方程式和能量微分方程式形式完全一致，且各自对应的边界条件也是相同的，说明边一71-73/245H四56，ll令K/s0◎0C83％□117：30P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.76Size:196！×传热学习题集和答案详……馨翼”传热学习题解答幸己m＝1，n＝2～12为绝热边界；t己，atse8＝液的n＝13，m＝1～5为绝热边界；008比，m.0取一8林，（m＝5，n＝2，12为绝热边界；面液已面望，诚中围m＝1，n＝2～12为绝热边界；（m）八W02式装皂的m＝3，n＝3～11为恒壁温80℃；nim0Enim1宝卧双0m＝4，5，n＝3，11为恒壁温80℃；其余为内部节点；△x＝24y，列出各节点方程编程求解得：1＝399入。点，款面长11，点中由更1＝入S△t＝入S（80℃-30℃），得此种情形下形状因子S＝7.98。01，20.烟道墙内、外壁分别维持在650℃和50℃，墙体由导热系数为1.4W/（m·K）的材料砌成。墙体尺寸及1/4角的网格划分如图5.18所示（见教材）。试确定节点1～6的温度分布及通过每米长该墙的热流量。如果内壁与温度为650℃、表面传热系数为100W/（m2·K）的流体接触，而外壁与温度与50℃、表面传热系数为25W/（m2·K）的流体接触，试重新计算温度分布和散热量。308＝【解】该题是一个二维稳态导热问题，△x＝△y＝0.5m。海中①当烟道墙内、外壁分别维持650℃和50℃时，编程求解得节点1～6的温度分别为325：12，300.24，175.84，303.11，336.60，343.30℃；通过每米长该墙的热流量为7424.7W。②当烟道墙内、外壁均为第三类边界条件时，编程求解得节点1～6的温度分别为333.16，306.64，186.00，310.01，346.26，353.74℃；通过每米长该墙的热流量为6948.3W。中生斯产空干由。级国二个一具女【精】点节中其，求谷斑家单衣图，置非一6668/245才K口H56l令K/S109⊙0C83％□17：31P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.07Size:179.×传热学习题集和答案详……第7章“对流换热的求解方法”习题解答00＝（r）＋（0）u＝dy0x0＝（）10-1:0＝已知n＝2f＝8＝（）:华宝量山果0alauafan＝/uvxf＇（n）（1）u＝gy-可nayu。_1uf＇（n），态一）＝-11（axax:火望式己卤帝县（-）＝--＝-22dxax上式中，一1336616，44630（）＝2xuvx036（2）0＝-1-（m）＋＝f（m）-U＝u（3）＝24（m）＝-n（m）6业0＝业（）--代入动量微分方程，得：b站，0＝日（宽朗）中量热试的内r己0一0，3果百本，【】＆unf＂（n）f＂（n）＋）（n）-2（）＝2（m）100＝（0＋0整理后的无量纲动量方程为：一73—75/245才KH田56l令K/S1040C83％□17：31P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:2.05Size:179.×传热学习题集和答案详……第7章“对流换热的求解方法”习题解答＝2.67×10-2W/（m·K）；v＝16×10-6m2/s；Pr＝0.701。ul10×0.5Re＝v-16×10-6＝3.125×103＜5×105属于层流03x＝0.5m时：＝h86，＝5xRe212＝5×0.5×（3.125×103）-12＝4.47×103m＝4.47mmC＝0.664Re21＝0.664×（3.125×103）-＝1.19×10-3h，＝0.332入Rep13r00.0＝塑阳emO1＝广空39Se＝，干大村。S齿成曲当0.332×2.67×10-20.5x（3125×10）-2×（0701）W/（m2℃）。系特亲进基猎品，是畏出些，奥碧是畏＝8.8W/（m2.℃）h＝2h-1＝2×8.8W/（m2.C）＝17.6W/（m2.℃）xE＝h（tn-t）A＝17.6×（40-20）×0.5×1W＝17.6W11.15℃的水以3m/s的速度外掠平壁，试计算距平壁前缘100mm处的边界层内的质量流量及流动边界层的平均厚度。【解】t＝15℃时，查教材附录5，p＝998.95kg/m3，v＝1.156x10-6m2/s按积分方程推导：：限为算谷庆态，01x01x00.F＝uu（）一（）0.＋＝80M＝fuy＝pu-［（）（号）门N98＝3-0112（）-（门（号）AA8E.0＝.1-）-30m·W）dram，3因6＝4.64Ta.er.I8202故M＝825ES.S0018Pux4.64＝2.9puvxEr.s027577/245H田56l令K/S1040C83％□17：31P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.14Size:188×传热学习题集和答案详……答输接传热学习题解答”幸菜f＂（n）＋ff＂（n）＝006m＝0:f＝0f＇（m）＝0→0：f＇（m）＝29.根据动量守恒定律，证明常物性流体在水平圆管中层流稳态流动时，流动充分发展段的动量微分方程式为：1a，0u）_1/prar）证明时坐标原点取在管中心线上，沿流向为x轴，径向为r轴。（【证明】由教材附录9知，常物性不可压缩流体轴对称二维稳态层流流动的N-S方程为：66x向：606pudx.-＋1（21＋＋p0--x＝A，中1r向：u，p＋6av＋purarpuaxar（m流动充分发展时：（＋（）--＝（5）v，＝0，0u＝0dx）三6（）”1I3（EG6p＝0，故ap_dedxdx06x向的动量方程简化为：V“（（＋）101012＝1reararax2udx16（2但＝0，故1＝（xr/udx，端量人10.压强101325Pa，温度为20℃的空气掠过温度为40℃的平壁表面，速度为10m/s。试用微分方程求解距前缘x＝0.5m处的6，Cx，h及0～0.5m内的对流换热量（壁的宽度取1m）。【解】，本题可直接应用分析解的结果。定性温度tm＝2（t＋t）＝）（）＋（）（2（20＋40）C＝30℃查教材附录4，则30℃时空气的物性参数为：A74一76/24518.90C83％□17：31P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.23Size:179.×传热学习题集和答案详……区”老传热学习题解答“净下团中水的1d8808、（代期）6＝8→6d8＝出长，量阳是泉平长积分：＝，末帕尘式身望大量的界】游8词不向式达面型末对就本美曲市代变山B.C:x＝06＝0c＝08m01x老00，0＝.00乙96与x的关系为：01x270e08120x＝3.464u-01x。5＝或6＝3.464Re-12xx15.应用连续性方程au＋au＝0和速度分布axay（）果并已知84.64，导出x/Re，的分布方程。900.0S28.0E00S020-y1008m）【解】由连续性方程可得：＝-raudy注意：6＝p（x），u＝f（6，y）＝f［p（x），y］氧改写速度分布为：u＝（6一/8）平au＝u138-21833-4d8＝4＝1-210＋20dx240（8-2-8）3do）（1）又6＝4.64＝AxnAu二，昨d6_14xn＝Ax12-8dx222x:，代用人）（2）式（2）代入式（1），得：（小是udx4x（）-（门:司食-78—80/245H田56l令K/s1660C83％□117：31P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:4.57Size:188×传热学习题集和答案详……第7章“对流换热的求解方法”习题解答13.平板长0.3m，以0.9m/s的速度在25℃的水中纵向运动，求平板上边界层的最大厚度，并绘出它的速度分布曲线（积分方程解）。【解】边界层的最大厚度发生在板的末端处，即x＝0.3m处。本题要求计算板末端沿壁面法线方向不同距离处的局部速度值，并描绘出速度分布曲线。25℃时，v＝0.9055×10-6m2/s0＝30＝8.0＝x:6mx＝4.64＝4.64x0.9055×10-6×0.3N0.9m＝2.55×10-3m＝2.55mmu＝588y-3×103y3u2（号）-（u＝529.2y-2.7×10y30＝计算结果如表所示：y/mm0.511.52.55u/（m·s-）0.2610.5020.7030.8420.902速度分布曲线略。三（8u.（）8：新14.若平板上流动边界层的速度分布为＂＝，求层流边界层厚8度与流过距离x的关系（按积分方程推导）。M6【解】动量积分方程见教材式（7.34），得：6可（1-）（）＝（已知速度分布为二，故u0＝81）（）代入积分方程，得：66［（号）（1-号）（号）vu。人升（S）质6积分后得：-7779/245H田56l令K/s5.30C83％□117：31P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.0Size:188.×传热学习题集和答案详……客特队”传热学习题解答＝2.9×998.95×√3×1.156×10-6×0.1kg/s＝1.706kg/s0121c.0X013＝.dx＝4.64xndx4.6402312×4.64121.156×10-6×0.13Vu3×4.64×＝301xm＝0.607×10-3m（0L×281E）x40.0＝9AA00.0＝3＝0.607mm80＝12.标准大气压力下，温度t＝52℃的空气以u＝10m/s的速度外掠壁温t＝148℃的平板。试求距前缘50，100，150mm处的流动边界层厚度、热边界层厚度、局部表面传热系数和平均表面传热系数。【解】定性温度tm2（＋1.）＝2（52＋148）C＝100C查教材附录4得空气的物性参数：＝3.21×10-2W/（m·K），v＝23.13×10＋6m2/s，Pr＝0.688。厘平mE帕21：当x＝150mm时，Re＝ux10×0.15＝（v23.13×10-6＝6.485×104＜5×103，故流态为层流。各计算式分别为：：早式姓：m06＝4.64＝4.64x23.13×10-x12＝7.06×10-3x12u6108＝8Pr-13＝7.06×10-30.68813x2＝8×10-3x129＝xb＝1h，＝0.332Rep1/3A＝0.3321＝p1OAx-12＝6.187x-12h＝2h，＝12.375x-12各局部点计算值列表计算如下：x/mm8/mm6，/mmh2/（W·m-2.℃-）h/（W·m-2.℃-1）501.581.7927.6755.341002.232.5319.5739.131502.733.1015.97831.957678/245118H田56l令K/s⊙0C83％□17：31P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.07Size:171.×传热学习题集和答案详……第7章“对流换热的求解方法”习题解答-［（）（dy/8＝（）1（号）-（门（）:，式由（）（）-（）16.由上题的推导结果证明任意x截面处，边界层外缘线上具有的最大值vmx。按第11题条件求出vm，并与u。比较。根据比较的结果进一步思考，在数量级分析中，如u～0（1），v～0（6）是否合理？【证明】23u二4（）-（）门d＝0，求得驻点为y＝6，极值点必然就是驻点，因此可以证明当y＝6时，v＝vmx，即边界层外缘线上具有v的最大值。按第11题条件，x＝100mm时：1.156×10-6×0.1＝b16＝4.64×3m＝0.91×103mVmax＝（10（1-）＝（）U1＝（3）bX1×10x3m/s＝5.12×10-3m/sb可见，vmx与u。比较，vmax小很多。因此，在数量级分析中，如取u～0（1）和v～0（6）是完全合理的。17.由边界层动量微分方程沿边界层厚度积分，直接推导出边界层动量积分方程式。【推导】已知边界层动量微分方程式为：（1）人分①，图uYh66dxay6从0～8积分，得：79—81/245H田56l令K/s187⊙0C83％□17：31P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:4.38Size:188×传热学习题集和答案详……答”传热学习题解答“幸audydy＝duedyusdx0110dy（1）axy①②8由连续性方程，得：（声（）-（月D＝（2）dx-18。将式（2）代入（1）式中第②项，得：四新果的蓝由0子yay60在避量喜，思一果令U＝1dy，dU＝audy，dvaydy，V＝u0故②＝-然心直姓，8＝元式热新束.0：Udv注意到微分法则，d（UV）＝Udv＋VdUmm00＝，料翼1订故的0x-0I×021但a（Uv）＝［UV］8＝1＝ya＝101×I0.010好②＝duau好，udv＝-u.ad（8）0一味（1）0一界好④-［。（），（）］果安由＝-ayl，-0用是运将②，④代入式（1），得：u--00uayly＝0整理并配方为：，一0月-80—82/245H田56，ll令K/s1190C83％□17：31P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.97Size:179.×传热学习题集和答案详……第7章“对流换热的求解方法”习题解答亚y12audy山jduddydxousdyvou造，03三下dx（3）ayly＝o注意到（记偏微分为常微分）:时类rudlo）采8（w.u-u）dy＝（autuau-2udAaxaxdywdx（u-u）dy＝auedy-山audyaxdx将微分符号提出积分符号外，得：duou（w-u）dydx（u-u）dy＝v（du康宝（4）aya0＝:（1Q00＝依查因Tx＝μu，式（4）可以改写为：（P.n）XWay/，＝01×2800m）三880.0XOdduou（-u）dy＋pa（）dy018.温度t＝80℃的空气外掠t＝30℃的平板，平板长为0.3m宽为0.5m，已知h＝4.4x-，试求对流换热量（不计板宽的影响）。C＝A【解】ah＝4x-1ndx＝I24.4＝01X8858.8l12＝8.8/√0.3W/（m2·℃）＝16.07W/（m2.℃）＝h（t-t）A＝16.07×（80-30）×0.3×0.5W＝120.5W19.空气以40m/s的速度掠过长宽均为0.2m的薄板，＝80℃，t＝120℃，实测空气掠过此板上、下两表面时的摩擦力为0.075N。试计算此板与空气间的对流换热量（设此板仍作为无限宽的平板处理，不计板宽方向的影响）。80×01×8【解】本题已知摩擦力，可采用类比关系式求解。注意给定的摩擦力为空气外掠薄板上、下两表面的总摩擦力。Q0＝5—81—83/245口H田56l令K/s1160C83％□117：32P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.39Size:188！×传热学习题集和答案详……传热学习题解答“幸h＝Nu入_1242.4×3.49×10-2W/（m2·℃）0.6＝72.27W/（m2·℃）＝h（tn-1）A＝72.27×（250-30）×0.6×1W＝9540W其中，层流区域的表面传热系数应为：×01×20小（0h，＝0.664·）WAJ8千263.49×10＋2×5×103×0.6841/3内登＝0.664×W/（m2·℃）平塑管（0.309EEi＝aHmm＝46.72W/（m2·℃）录前类用起达盛世平层流换热量：①＝h（t-t）A1＝46.72×（250-30）×0.309×1W＝3176W湍流换热量：中，＝-中1＝9540W-3176W＝6364W外寒E23.临界雷诺数Re。＝3×103，试推导出代替Nu＝（0.037Re8-870）P13的外掠平壁湍流平均换热准则关联式。量聚代【推导】外掠平壁湍流换热时，如壁面足够长，壁前面部分为层流区域，x。以后发展为湍流区域，全壁长范围内的平均表面传热系数应按层流段和湍流段以加权平均的方法求解。1:变感宝010～x，层流：h＝0.332Rep1△＝Ax-12，其中A＝0.3322VV88.0＝79:201x85＝:（m；x。～l，湍流：h，＝0.0296Re08pr13入＝Bx-15，其中B＝0.0296H×8.SX01x80.8A0＞m008.0＝mPr3。考虑到层流段的影响后，平壁湍流边界层平均表面传热系数计算式为：0.001x159159h＝（＋）8.TSATE0.0）＝M其中￥.S01280.0×［008-（01x17）80.0］＝84-86/245H田56l令K/s1160C83％□117：32P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.20Size:196×传热学习题集和答案详……第第7章“对流换热的求解方法”习题解答hp23＝5.54x107OIxFpcpum故h5.54×10-pcpm（子.m）八TT＝Q＝WPr23.0×H0E0）×8T＝（.）A＝5.54×10-4×0.3335×4198×20中其W/（m2·℃0.494＝31.4W/（m2·℃）00.0＝21.水流以1.3m/s的速度通过内径19mm、长为5.5m的管子，压降为42mmHg（1mmHg＝133.322Pa），管壁平均温度为80℃，管内水的平均温度为55℃。试用类比律求表面传热系数。＝【答】h＝7054W/（m㎡·℃）量性魅园22.在一个标准大气压下，温度为30℃的空气以45m/s的速度掠过长为0.6m，壁温为250℃的平板。试计算单位宽度的平板传给空气的总热量、层流边界层区域的换热量和湍流边界层区域的换热量。＝3x10时嘉园9（058县【解】面本题平板前面为层流区域，后面为湍流区域，应先求出分界点，然后按相关准则关联式计算。，定性温度：tm＝（t＋tw）＝（30＋250）℃＝140℃谢迎查教材附录4，干空气的物性参数为：入＝3.49×10-2W/（m·℃）；v＝27.8×10-6m2/s；Pr＝0.684。Re。＝v＝5×105故x。＝5×103v5×103×27.8×10-6m＝0.309m＜0.6mu45因此，边界层的流态为：0≤x。≤0.309m为层流；0.309≤x。≤0.6m为湍流。ul45x0.6393×10W为27.8×10-6＝9.71x103Re＝Nu＝（0.037Re8-870）P13＝［0.037（9.71×103）0.8-870］×0.68413＝1242.4中其—83—85/245H田56l令K/s1080C83％□17：32P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.91Size:188.×传热学习题集和答案详……第7章“对流换热的求解方法”习题解答h.dxAxindx＝2Ax2x＝Bx＝2B（-）穿站故＝242＋B（-x）m0x0×8＝:站，＝0.664RePr3X＋0.037（Re98-Re8）Pr1/3入麻N--（0.60.037-037）＝（0.037Re8＋0.664Re！-0.037Re8）Pr13取Re。＝5×103时，Re2＝707.1，Re.8＝36239，代入上式，整理后得：，前付用Nu＝（0.037Re0:8-870）P，1/3取Re。＝3×103时，Re＝547.72，Re8＝24082.25，此时：内同B，相Nu＝（0.037Re8-527）P1324.在一台缩小成为实物的1/8的模型中，用20℃的空气来模拟实物中平均温度为200℃的空气的加热过程。实物中空气的平均速度为6.03m/s，问模型中的流速应为多少？若模型中的平均表面传热系数为195W/（m2·K），求相应实物中的值。在这一实验中，模型与实物中Pr并不严格相等，你认为这样的模化实验有无实用价值？【解】对于空气受迫流动换热，Pr可近似视为常数，故Nu＝f（Re）。要使模型实验结果能够推广使用，必须符合物理现象相似条件，同名相似准则必须相等，即Re1＝Re2ot1＝20℃时：v1＝15.06×10-6m/s2，入1＝2.59×10-2W/（m·℃），Pr1＝0.703；t2＝200℃时：v2＝34.85×10-6m/s2，2＝3.93×10-2W/（m·℃），P12＝0.680。（）左题，醉态浴。处时不态清管由于ua2l2V1V2-85一87/245口H四56，ll令K/s1060C83％□17：31P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.64Size:171.×传热学习题集和答案详……答联区”志传热学习题解答“幸F0.075T＝A-2×0.22N/m2＝0.9375N/m1但Tw＝2Cp，故p6采用Colburn类比律：常长食5）面意StPr23CTweb/62T2（9-b3uC-6hpr2s＝Tpus6b（-sM）P.2xhTwh＝是脊用出号端部定性温度：5tm（＋。）＝（120＋80）℃＝100℃查教材附录4，cn＝1.009kJ/（kg·K）；Pr＝0.688，故h＝TC0.9375x1.009×1因uP23.40×0.68823W/（m2.℃）＝30.32W/（m2.℃）＝h（tn-）A＝30.32×（120-80）×0.22×2W＝97W20.煤气以平均速度um＝20m/s流过内径d＝16.9mm、长l＝2的管道，由于不知道它的表面传热系数，今实测得管道两端煤气的压降△P＝35N/m2。试问能否确定煤气与管壁的平均表面传热系数。已知该煤气的物性为：p＝0.3335kg/m3，c，＝4.198kJ/（kgK），v＝47.38×10-6m2/s，入＝0.191W/（m·K）。【解】本题已知压降△p，可采用类比律求得h。三88d2飞0X16.9×10-308）X201＝1（-1d＝①∫＝Apx＝＝35x20.3335x202X＝4.434×10-3pumSP23＝4.434x10-空，子0S1:投则T8081＝5.54×10-4Pr＝兰＝VPC47.38×10-6×0.3335x4198宽进不，里＝0.347宝意a入关的类月0.191展日P23＝0.494氏率总面秀两，处药就空武式—82—84/245H田56l令K/s2400C83％□117：32P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.53Size:180.×传热学习题集和答案详……答联”传热学习题解答便章故V22又＝8，_15.06l2-＝0.432l1＇v234.85＝b故模型流速为：us1＝8×0.432x6.03m/s＝20.85m/s9＋＝1和2属于彼此相似的现象，因此Nu1＝Nu2，即丝，故：入1入280.0＋08200.0）＝＝Mh2＝l217W/（m2.℃）员000＋803月80.0）＝＝40W/（m2·℃）80只ror空气的P数变化不大，模化实验遵循相似理论的基本原理，可推广使用到P·数近似相等的流体换热现象中，具有实用价值。25.两根管子，a管内径为16mm，b管为30mm，当同一种流体流过时，a管内流量是b管的2倍，已知两管温度场完全相同，问管内流态是否相似？如果不相似，在流量上应采取什么措施才能相似？【解】流态相似，必然有Re1＝Re2。由题意知，温度场完全相同，umldum2d2故一2，或者uada，即边的中，m0，0式更V，中一k（Mr）NWcQ器dh30_15ud168用试不（（1）M站，常比财蛋面但Q。＝2Q6，Q＝du，即，命果翅炎女变。（入1，等讯心划卧含同，书（，m）八V01xec4mdu＝21＝：0＝3u。211512-15605.0＝，（·m）0aud28）8＝4:1000＝故管内流态不相似。欲使流态相似，必须满足式（1）条件，即_.dubQdada干由—86—88/245H田56l令K/s240083％□17：32P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:2.97Size:180.×传热学习题集和答案详……第7章“对流换热的求解方法”习题解答故Q.d.8香9＝1主Qd015夏面泰始货【】26.夏季的微风以0.8m/s的速度沿宽度方向掠过一金属建筑物壁面，壁面高3.6m、宽6m。壁面吸收太阳能的热流密度为350W/m2，并通过对流换热把热量散发给周围的空气。假设外掠壁面的空气温度为25℃。试计算在平衡状态下壁面的平均温度。：【解】由题意知，热平衡状态下应有：005.0＝19辐射得热q.＝对流换热qc实因tw未知，物性参数不能确定，本题可采用试算法进行。设。＝275℃，＝2（＋t）＝150℃，查教材附录4，空气v＝28.945×10-6m2/s，入＝3.565×10-2W/（m·℃），Pr＝0.683。Re＝ul0.8×6v28.945×10-6＝1.658x103＜5×10属层流Nu＝0.664Re12Pr13＝0.664×4.07×0.88＝238三。h＝238×3.565×10-26XW/（m2·℃）＝1.42W/（m2·℃）9.0＝h（t-t1）＝1.42×（275-25）W/m2＝355W/m2计算表明，当t＝75℃时，可求得h＝1.44W/（m2.℃），因此t对h的影响不大，本题可按h＝1.42W/（m2·℃）计算，由热平衡方程可求得：501x2S01×01x.9×01＋01x×350tw＝tr＋q三25℃＝271.5℃己1＝h1.42A＝①故热平衡状态下，壁面的平均温度t＝271.5℃。27.有人设想把南极的冰山拖运到10000km以外的干旱地区以解决淡水供应。设冰山可视为长1km，宽0.5km，厚0.25km的大平板，拖运速度为1km/h。途中冰块与海水、冰面与空气的平均温差均为10℃，忽略冰面的辐射换热，试估计冰山拖运中水上与水下两部分的融化量及其比例（已知Re＝5×103，溶解热为3.34×103J/kg；计算中可将冰块的侧面积全部归于水下部分；海水与冰换热时的物性按纯-87—89/245口H田56l令K/s19100C83％17:32P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.59Size:188×传热学习题集和答案详……答”传热学习题解答“幸数据并确定准则方程式中的系数。⑦现有一根长圆管，d＝80mm，管内空气速度为28.9m/s，t＝150℃，t＝50℃，试确定管内换热现象与上表中哪个现象是相似的？并用上表实验结果确定此管内的表面传热系数。⑧又一未知流体的换热现象，已知其a＝30.2×10-6m2/s；入＝0.0305W/（m·℃）；v＝21.09×10-6m2/s；d＝65mm，管内流速23m/s。它是否与上表中的实验现象相似？是否可以用上表实验结果来计算它的表面传热系数？为什么？如果能用，请计算其Nu数和表面传热系数。长管内空气换热实验数据表实验点tn/℃t/℃u/（m·s-）h/［W/（m2·K）］d/mm130103.0115.050250108.0031.5503-701017.057.550A901035.910650【解】①空气稳态受迫对流换热，空气Pr三常数，Nu＝f（Re），因此该实验涉及的相似准则为Nu和Re。②Re＝undNu＝hd物性参数，可由定性温度查出，因此需测01入量um，d，h。其中h由测量结果计算得出。③列表计算如下：器液职目定性V×106A×102实验点u/（mh/（W·m-2温度（m2/（W·m1.d/mmReNus-1）1℃s-）℃）℃-）2015.062.593.01501510428.963016.002.678.005031.52.5×10458.994016.962.7617.005057.55×104104.1745017.952.8335.905010610187.28些星来五盛式顺阳公09092/245H田56，ll令K/s1910C83％□117：32P:0/1dX:-9.8dY:-0.8Xv:-0.487Yv:0.001Prs:1.72Size:188.×传热学习题集和答案详……第7章“对流换热的求解方法”习题解答，im＝0.329W/（m2·℃）。嫂系的中无长新宝戏贝中＝hn△tA2＝0.329×10×5×103W＝1.645×10°W空内面支融解速率：果烫皇个中己中。1.645×106术又8。茶好m三ym3.34×10kg/s＝4.9kg/s0800水下融解量所占比例为：8C麻认其mw公针武好系计面帕真十味果71＝-＝99.93％m＋m系面水上融解量所占比例为：突燕尸空内ma＝0.07％弹地2＝m.＋mw假设融化过程是在上、下两表面进行的，即拖动过程中由于冰块融化仅减小了其厚度，则每小时冰块的融化量为：O5M＝（m＋mn）×3600＝2.54×10kg/h00冰的密度：P；＝920kg/m3（查教材附录2）冰块的总质量为：M＝V＝920×103×5×102x2.5×102kg＝1.15×10kg融化时间为：需业因，出查盛M4宝1.15×10，bT＝M＝2.54×10-h＝4.53×103h于果量由中其。。b.x到达目的地所需的托运时间为：L_104h＝v1m·W八。m）比较可见，T＜T，因此该设想不成立。28.在相似理论指导下进行试验，研究空气在长圆管内稳态受迫对流换热的规律，请问：①本项实验将涉及哪几个相似准则？②试验中应直接测量哪些参数才能得到所涉及的准则数据？③现通过实验并经初步计算得到下表所示数据，试计算各实验点Re数及Nu数。④实验点1，2，3，4的现象是否相似？⑤将实验点标绘在lgNu及lgRe图上。⑥可用什么形式的准则方程式来整理这些数据？试整理这些一8991/245H田56l令K/s160083％□17：32P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:2.52Size:171.×传热学习题集和答案详……传热学习题解答章水计算）。【解】设冰的表面温度为0℃，则定性温度tm＝5℃。查物性参数表，得：金一食常的am80风婷季夏冰水：w＝56.25×102W/（m2·℃），v＝1.5475×10-6m2/s，Pr。＝11.6；好于空面鼠合货赠是燕界族叔威氏，mW空气：入＝1.475x10-2W/（m2·℃），vn＝13.72×106m27s，Pr＝0.706。:不态处衡平基，联意级由【拖运速度：0＝0根晶1000＝0.278m/s眼本，面不，低未因u＝3600冰面与水之间：查，子01＝（＋1Rewul0.278×103＝1.8×108＞Re。属湍流10.85vw1.5475×10-6×80冰面与空气之间：＞0×8花0三901080ul0.278×103Re＝-13.72×10-6＝2.03×10＞Re。属湍流00Nu＝（0.037Re8-870）P/3＝3.348×10Nun_3.348x103x56.25x10-2hw＝lW/（m2.℃）10尚因＝188.3W/（m㎡·℃）冰面与水的对流换热面积：A＝（103×5×102＋103×2.5×102＋5×102×2.5×102）m2＝12.5×103m2中＝h△tA＝188.3×10×12.5×105W＝2.354×10°W中w2.354×109融解速率：m＝y3.34×103kg/s＝7.05×103kg/s半大冰面与空气的对流换热面积：A＝103×5×102m2＝5×105m2中宝Nu＝（0.037Re.8-870）Pr＝2.23x104的面题，丁01：还量冰题的h，＝Nun入2.23×104×1.475×10-2W/（m2.℃）—88-90/245H田56，l令K/s95.50C83％□17：32P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.29Size:188×传热学习题集和答案详……第7章“对流换热的求解方法”习题解答④4个实验点均属同类现象，单值性条件相似，但Re准则不相等，因此彼此不相似。0XP0.19⑤lgNu-lgRe如图所示。庭类且，戏调室已.0＝4B三式因，草节世米为3）×581098％878100＝7L（m）Wc00×S！，0colgRe⑥实验结果可整理成幂函数的形式，即Nu＝cRe＂任取直线上两点A，B，量得L1＝32，L2＝40，所以：ntana＝＝0.8点1、点4均近似在拟合直线上。Nu1＝0.0183，c4＝ReCIResNu4.8＝0.019取平均值：c2（1＋c4）＝0.0187所以，准则方程式可写成：Nu＝0.0187Re0.8本题可用最小二乘法整理实验数据，获得更为合理的结果。1⑦t＝（t＋tn）＝12（50＋150）℃＝100℃查教材附录4，v＝23.13×10-6m2/s；入＝3.21×10-2W/（m·℃），则umd28.9×80×10-3Re＝V80×10-3＝103＝Re4该管内的受迫流动换热现象与上表中的现象4是相似的，所以Nu＝Nu4＝187.28，则Nu4入187.28×3.21×10-2h＝d80×10-3＝75.15W/（m2.℃）—91—93/245口67田56，l令K/sO83％-17:32P:1/1X:843.5Y:50.2Xv:-0.148Yv:0.222Prs:3.85Size:179.×传热学习题集和答案详……区“传热学习题解答幸und_23×65×10-3同思皮点个⑧Re＝v～21.09×10-3＝7.09×104不班国与4个实验点Re均不相等，因此彼此不相似。但可用准则方程式来进行计算，因为Pr＝”＝0.7与空气的Pr数近似，且属同类现象，单值性条件相似。Nu＝0.0187Re0.8＝0.0187×（7.09×104）0.8＝142Nu4入142×0.0305h＝-d65×10-3W/（m2.℃）＝76.5W/（m2.℃）明，先函里顶果雀剑＇slo＝aM:均.0＝d，三量，8，E点两直直合政4点1点，80＝一二010.0-＝0，810.0＝810.0＝（20＋（0）＝3:直平”8100三M:官发联长，果始合式更群落，嫂鲤取生乘二小用口本3001＝3（021＋02）片＝（＋）50×15.8＝A；8、m°O1xEF.EC＝4，查，（3m）八2＝01＝0108×0.8501×08演，的麻县斑的中上民泉艇受内海.8.81＝A＝6m）Wc＝01x18.x85.581人01×089294/245口67H田56l令K/s⊙0C83％C□17：32P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.39Size:196.×传热学习题集和答案详……区“传热学习题解答快素und23x65×10-3同皮点个①⑧Re＝v～21.09×10-3＝7.09×104不业国与4个实验点Re均不相等，因此彼此不相似。但可用准则方程式来进行计算，因为Pr＝＂＝0.7与空气的Pr数近似，且属同类现象，单值性条件相似。Nu＝0.0187Re0.8＝0.0187×（7.09×104）0.8＝142Nu4入142×0.0305h＝-d65×10-3W/（m2.℃）＝76.5W/（m2.℃）明，先函里果雀剑突＇slo＝aM:均.0＝d，6三量，8，两直寒主直合点点，8.0二0＝1P0.01-0，E810.0＝7810.0＝（20＋（0）＝2:平aT810.0＝M:如，果常合式更界落，银嫂望美取当二小讯口本3001＝3（021＋02）＝（＋，）＝m0×15.8＝A:8m°（1xEF.EC＝4，A妹查闽，（·m）NW2＝301＝01×08×.8bm5三品01×02演，的麻县斑的中上民泉艇恒受内海8S.F81＝A＝76m）Wc＝01x18.x85.581人一01×089294/245HD56，l令270K/sC83％□17：33P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:2.69Size:171.×传热学习题集和答案详……第8章“单相流体对流换热及其实验关联式”习题解答的层流流动换热是否能采用光滑管公式计算？为什么？【答】流体力学对粗糙管壁内的流动进行了大量的实验研究，积累了大量的摩擦系数实验数据。因此，粗糙管内的换热计算可以采用类比公式，即SP2＝f/8来进行计算。当缺乏阻力数据，不能采用类比公式进行换热计算，且无实验获得的粗糙管内准则关联式时，可采用光滑管实验关联式进行换热计算。但关联式计算结果必须乘以粗糙管壁修正系数k且e＞1。当粗糙管内的流态为层流时，由于糙粒高度被边界层所覆盖，其强化传热的作用已消失，故可采用光滑管公式进行计算，结果勿需修正。燕找补前式得代量来前5.管内受迫对流换热时，对于横管和竖管中流体被加热和被冷却，自然对流的影响各有什么不同？什么情况下应考虑自然对流对受迫对流的影响？计小花风界张曲8至8电【答】对于横管，流体不管被冷却还是被加热，都将有利于换热。因为当横管中流体被冷却时，由于管心温度高于管壁，将形成管心向上而沿管壁向下的垂直于受迫流动方向的环流；而当横管中流体被加热时，由于管心温度低于管壁，将形成由管心向下而沿管壁向上的垂直于受迫流动方向的环流；由于都形成了环流，加强了边界层的扰动，所以都将有利于换热。答对于竖管，当流体向上流动时，如果流体被冷却，则在管中心受迫对流与自然对流同向，而靠近壁面处两者方向相反，这样管中心的速度比原来的大，而管壁面处则比原来的小，不利于换热；如果流体被加热，则自然对流与受迫对流同向，有利于换热。当流体向下流动时，则自然对流对换热的影响与流体向上流动正好相反。如流体被冷却，则自然对流与受迫对流同向，有利于换热；如果流体被加热，则在管中心受迫对流与自然对流同向，而靠近壁面处两者方向相反。这样管中心的速度比原来的大，而管壁面处则比原来的小，不利于换热。至于什么情况下应考虑自然对流对受迫对流的影响，可通过惯性力和浮升力数量级的对比进行判断，一般，当Gr/Re2≥0.1时，就应考虑自然对流的影响。6.传热学中通常把“管内流动”称为内部流动，将“外掠平板”、—95—97/245口H田56l令K/s120⊙0C83％□17：33P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.67Size:188×传热学习题集和答案详……塑内明可典因，身都子空内室高脉塑内，夏，卤自第8章“单相流体对流换热及其实验关联式”习题解答副面东水鼠长因，小划一：季两1.对于Pr＞1的流体管内层流受迫流动换热，参照教材图8.1a试定性地画出流动边界层和热边界层的发展示意图，并标示出热入口段与流动入口段。部味回空达因部：【解】P＞1时，流体的动量传递能力大于能量传递能力，因此流动边界层更早地在管中心汇合，表现为L，＞L，边界层的发展示意图如下图所示：其高其，式一窗圆：产空内室！器装始垃.L-管如前内音灯大更惠是（第1题图）高嫂面麦的小图中：L为流动入口段长度，L为热入口段长度。可见P＞1的流体，L＞Lo2.试定性分析下列问题食应扑用采公春贝遗图断①夏季与冬季顶棚内壁的表面传热系数是否一样？量漫闻②夏季与冬季房屋外墙外表面的表面传热系数是否相同？③普通热水或蒸汽散热器片型高或矮对其外壁的表面传热系数是否有影响？④从传热的观点看，为什么散热器一般都放在窗户的下面？⑤相同流速或者相同的流量情况下，大管与小管（管内或管外）的表面传热系数会有什么变化？林代【解】①答：不一样。因为空气是热气流向上运动，而冷气流向内肤录菜肤面和—9395/245口H56，l令270K/sC83％□17：33P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.15Size:196！×传热学习题集和答案详……”是关传热学习题解答补单幸8“外掠圆管”称为外部流动，试说明它们的流动机制有什么差别。这些对流换热问题的数学描述有什么不同？联板学【容【答】它们的流动机制的差别在于管内流动，其流体的发展受到管内空间的限制；而外掠平板或外掠圆管，其流体的发展不受外界的限制。这两类对流换热问题的数学描述的不同之处在于：①定型尺寸不同，如管内流动，定型尺寸选用管内径，而外掠平板，定型尺寸选用板长，外掠圆管定型尺寸选用管外径；②由于内流动受到流动空间的限制，除流动入口段以外，边界层理论不适用于流动充分发展段，因此不能采用数量级分析的方法简化对流换热微分方程组；③边界条件的描述也不相同，内流问题应考虑流动与换热的对称性。受内受7.对于竖壁表面的自然对流，当P＞1时，仍有6＞8，自然对流是因温差引起的，但，至6的流动边界层区域并不存在温差（温度近似等于t），为什么流体仍然存在着流动速度？【答】这是由于流体黏性力的拖拽作用，使未被加热的流体沿壁面向上流动的原因。8.什么情况下可以把竖直夹层内空气的自然对流换热作为纯导热过程？为什么？【答】当两壁的温差与夹层厚度都很小时，可以把竖直夹层内空气的自然对流换热作为纯导热过程。在这种情况下，自然对流非常微弱，以致可以认为夹层内没有流动，因此可以作为纯导热处理。实验研究证实：当以厚度6为定型尺寸的Gr＝ga△83/2＜2000时，可以作为纯导热过程，并以此作为判据。9.常物性流体管内受迫层流稳态流动，在流动充分发展段，描述流体运动的动量微分方程为：r/uax。根据微分方程，结合边界条件，证明流动充分发展段的速度分布为：u＝20.12-（门其中，R为管内半径。总送兄公干至【证明】数学描述为：一，计数饮爱量嫂比长城1a（au印如自惠平”，rrar东μax常服中学卧9698/245HD56l令2.5K/sC83％□17：33P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.38Size:196！×传热学习题集和答案详……传热学习题解答下运动，对于夏季，顶棚内壁温高于室内空气温度，因此夏季顶棚内壁处空气被加热而处于停滞状态；对于冬季，顶棚内壁温低于室内空气温度，冬季顶棚内壁处空气被冷却可向下运动，从而形成较强的自然对流。所以，冬季顶棚内壁的表面换热系数远高于夏季。②答：一般不相同，因为虽然夏季和冬季房屋外墙外表面的温度均高于室外空气温度，自然对流的规律相似，但表面传热系数是否相同还取决于房屋外表面与室外空气温度之差等因素，此外，夏冬两季室外风速也不相同，对表面传热系数的影响不同。出画服宝③答：有影响。因为空气在翅片间流动，起始段表面传热系数较高，稳定段相差不大。因此，起始段相同时，矮翅片的平均表面传热系数高于高翅片的平均表面传热系数。合中普早重表④答：因为窗户一般为玻璃，其导热系数远高于其他围护结构，导致在冬季其内表面温度较低，当其低于室内空气的露点温度时，易在窗玻璃的内表面结露。如果把散热器放在窗户的下面，由于室内空气通过散热器后的空气温度较高，可提高窗玻璃内表面的温度，从而有效防止结露的发生。⑤答：在相同流速或者相同的流量情况下，对于管内或管外流动，小管的表面传热系数高于大管，且相同流量时影响更大。以管内流动为例，按迪图斯-贝尔特公式，相同流速时，表面传热系数与d-成正比；相同流量时，表面传热系数与d-1.成正比。3.迪图斯-贝尔特公式采用什么方式来修正不均匀物性场对换热的影响？请分析修正方法的合理性。个【解】迪图斯贝尔特公式的两个表达式为系潜面Nu＝0.023RePr0.4加热流体普0.3冷却流体式中，用P＂来修正不均匀物性场对换热的影响。当加热流体时，n＝0.4；当冷却流体时，n＝0.3。显然，加热液体时由于壁面附近液体黏性降低，边界层内速度分布变得平缓，速度梯度增大；同理温度梯度也增大，h增大，n取0.4是合理的，符合h增大的特征。4.怎样计算流体在粗糙管中流动时的表面传热系数？粗糙管内94-96/245口H田56l令K/s1050C83％□17：33P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.57Size:196！×传热学习题集和答案详……第8章“单相流体对流换热及其实验关联式”习题解答00E00＝「r＝0duIE＝0B.C:2r8r1，or＝Ru＝0真（118）左林娃田来在流动充分发展段：p＝f（x），u＝f（r），故d业。＝q＝dxdxx2Q18微分方程改写为1d1）＝业rdr（rdr）udx88＝0＝0两次积分并代人边界条件后，可求得速度分布为：）081＝入（-出［-（门（1）平均速度定义为：（-01×S1）×82R88ETurdr）（188＝um＝R2。（2）将式（1）代入式（2）积分，可得：＝量燕：式平鼎由R2dp8udx将上式表示的平均速度代入式（1），可得速度分布为：＝中其（08-08）AE.OQu＝2011-（门3×180.0得证。10.润滑油以0.0315kg/s的质量流量在直径为12.7mm的管内流动，油温从93℃被冷却到67℃，管子内壁面温度为20℃。试计算满足冷却要求所需要的管长。【解】本题为冷却问题，需注意热平衡方程：流体放热量＝对流换热量。升鼠采，副望货勋国，部氏本奔宝前望定性温度：t＝1（＋）＝真卡（93＋67）℃＝80℃（8F＋2查教材附录8查得：c，＝2.131kJ/（kg·℃），入＝0.138W/（m·℃），v＝37.5×10-6m2/s，Pr＝490，p＝852kg/m3，则.tee＝0udMd4M（X·m）W01x1.00＝Rerpfu180.0..8e9799/245口H田56l令K/s2410C83％C□17：33P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.50Size:163×传热学习题集和答案详……区“爱半传热学习题解答补单”84×0.03153.14×12.7×10-3×852×37.5×10-6＝99＜2300属层流采用教材式（8.11）计算，此时：＝M＝PV1＝852×37.5×10-6N·s/m2）＝:想资山靠消＝3.195×10-2N·s/m2Hw＝pv＝887.5×2261×106＝2014Na，＝186（R·P）（）（）会提血入升来期两＝1.86（99×490）（）3.195×10-20.142＝38（）h＝3（台）（）＝38×0.138×（12.7×10-3）-23L-1/3＝96.34L-13由热平衡方程：流体放热量＝对流换热量，即（S）人外（）左Mc（t-t）h（t-t）mdl其中t＝（＋），代入参数值有：人）不0.0315×2.131×103×（93-67）-＝96.34（80-20）×3.14×12.7×10-3×L23解得：L＝20.8m，h＝35W/（m2·℃）。2180.0。0111.4.5℃的水以90kg/h的质量流量进入直径为100mm的管子，在流经3m长的距离流出时水温为38℃。试求管壁温度。【解】本题壁温未知，在采用准则方程式计算表面传热系数时需由壁温确定流体动力粘度，因此可假设壁温，采用迭代法逐次迭代计算。008＝（0＋更宝定性温度山（＋）＝-（4.5＋38）℃＝21.25℃:钱8袁林p＝997.9kg/m3，cp＝4.182×10-3J/（kg·K）a01×8＝入＝60.1×10-2W/（m·K）bibuu＝978.7×10-6N·s/m2，v＝0.981×10-6m2/s，PT＝6.82—98—100/245H四56，ll令K/s00C82％□117：39P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.84Size:180.×传热学习题集和答案详……第8章“单相流体对流换热及其实验关联式”习题解答:）大用采划，1＝1△午由厂一、AES0.0＝V人Mc.正dxdx9dxh（-t）mddx·:氏平由h（t-t）Tddx图中，管内气体的质量流量及其电加热量分别为：:M＝pumX191＝2R热平衡方程为：dx＝［h。（tn-t）＋h；（t-t）］ddx（t-t），ndMcpdx式中：h，h。分别为管内、外的表面传热系数，t为室温。14质量流量为0.5kg/s的流体流过一个内径为25mm，长15m的直管道，入口水温为10℃。管道除了人口处很短的一段距离外，其余部分每个截面上的壁温都比该截面上的平均水温高15℃。试计算水的出口温度，并判断此时的热边界层条件。【解】·由题意知热进口段很短，除此以外，任一截面壁温均比平均水温高15℃，符合ddi29＝常数的条件其温度的dxdxdxpcpumR变化规律均为线性规律（参考教材图8.4a），因此可判定本题属于常热流边界条件。由于出口温度未知，仍需假设，然后迭代计算。设＝90℃，1＝2（＋）＝50℃，查教材附录5，得p＝988.1kg/m3，cp.f＝4.174×103kJ/（kg·K），入＝0.648W/（m·K），v＝0.556×10-6m2/s，Pr＝3.54，则und4Mmno试至4×0.5920801Rer＝pndo-988.1x3.14×25×10×0.556x10-60＝4.64×104属于旺盛紊流。卧，丹杀界盛塑常否最金不本【】-101—103/245H田56l令K/s111C83％□117：33P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:3.67Size:171.×传热学习题集和答案详……跳区”郑关传热学习题解答补卧单”8逐次迭代，求得t＝89℃。本题中μ对表面传热系数的求解影响不大，因此迭代收敛很快。本题仅迭代3次即可求出壁温。12.流体在管内流动而被加热，已知管长L，m；管径d，m；管内流体质量流量M，kg/s；进口温度t，管壁为常热流边界条件，热流密度为q，W/m2。请写出计算表面传热系数h及管子进出口端壁温t，t“的详细步骤。9）08，1＝5【解】计算步骤为：①由热平衡方程，Mc，（t4-t）qmdL，假设t“→确定定性温度t＝2（＋）→由物性参数表查得c。→代入热平衡方程求出→比较假设值与计算值。若不相等，继续假设计算，最终求出真实。如流体为水，c，＝4.18×103J/（kg·K），空气可取cn＝1000J/（kg·K）。由于c，随温度的变化不大，假设计算1～2次即可计算出真实t②将1（4＋）作为定性温度，查得流体的物性参数。由（1-）＝1-”③计算Rer，判断流态。④根据流态，选择实验关联式，求h。⑤由q＝h（t一t）求出tn。注意tn为平均值，即t（＋）。10x＋18X000⑥常热流边界条件下，在热充分发展段，d，说明t。和tdx随x的变化规律相同，均为线性变化规律，因此：，眠米干由tw-te＝t-t＝t＂-t查，0＝好面可以求出t，“。严格地说，以上关系仅适用于热充分发展段，但对于长管误差不大。13.以薄壁不锈钢管作导体通电加热在管内流动的气体，管子裸露置于室内，试写出在稳态情况下，该管长dx微元段的热平衡关系。已知钢管电阻为R，Q/m，电流为I，A。【解】热平衡关系如图所示，热平衡关系式应为：通电加热量＝钢管外表面与室内空气的对流换热量＋钢管内表面与管内气体的对流换热量-100—102/2450口H田56l令K/s1150C83％□17：33P:0/1dX:0.0dY:0.0Xv:0.0Yv:0.0Prs:1.40Size:179.×传热学习题集和答案详……第8章“单相流体对流换热及其实验关联式”习题解答来M系4Mu4×9038m/s＝3.2×10-3m/spfprd997.9×3600×3.14×0.12Re＝und3.2x10-3×0.＝326＜2300属层流0.981×10-6团，盛塑微口出系面登出，pN，＝.6（RexPri）（）（）0.140.14＝1.86×326×6.82x1”（式平盘由①好出＋一出来铅香由一＋0.14＝7.81量，货婚，时不装直夏好（