ABC223（F，G）

F - Parenthesis Checking一直想做这种区间判括号序列合法性的题，但是一直不会，现在总算遇到了。首先，合法的括号序列的特征就是：序列

F - Parenthesis Checking

一直想做这种区间判括号序列合法性的题，但是一直不会，现在总算遇到了。

首先，合法的括号序列的特征就是：序列从前往后遍历，右括号的数量总不大于左括号的数量，且最后左右括号的数量相同。

那么很明显的处理方法是，将左括号视为 ，右括号视为 ，然后在遍历序列的过程中，观察前缀和是否为负，且区间和是否为 。

那么如何快速的处理多个询问呢？

考虑到区间和，前缀和，区间前缀最小值，都具有区间合并的性质，那么我们用线段树来维护信息。

那么我们判断合法性，就是，区间最小值不小于 ，区间和为0。

考虑如何维护区间前缀最小值和区间和。

区间和就是相加。区间前缀和最小值呢？考虑两个区间合并为一个区间 ，前一个区间的最小值保持不变，后一个区间的最小值即为前一个区间的区间和加后一个区间的最小值。

考虑每次修改为修改到根节点，每次 涉及的区间都会被更新，可在合适的复杂度内完成修改。

const int maxn=2e5+100;n#define ls ti<<1n#define rs ti<<1|1n#define midt(l+r>>1)nint n,m,a[maxn];nstring s;nstruct tree{n int l,r,sum,f;tn}t[maxn<<2];nvoid pushup(int i){ntt[i].sum=t[ls].sum+t[rs].sum;ntt[i].f=min(t[ls].f,t[ls].sum+t[rs].f);n}nvoid build(int i,int l,int r){ntt[i].l=l;tt[i].r=r;ntif(l==r){nttt[i].sum=t[i].f=a[l];nttreturn;nt}ntbuild(ls,l,mid);tn build(rs,mid+1,r);ntpushup(i);n}nvoid update(int i,int x){ntif(x>t[i].r||x<t[i].l)treturn;ntif(t[i].l==t[i].r){nttt[i].sum=t[i].f=a[x];nttreturn;nt}ntupdate(ls,x);n update(rs,x);ntpushup(i);n}ntree query(int i,int l,int r){ntif(l<=t[i].l&&t[i].r<=r)treturn t[i];ntint M=(t[i].l+t[i].r)>>1;ntif(l>M)tttreturn query(rs,l,r);ntelse if(r<=M)treturn query(ls,l,r);ntelse{ntttree ans,L,R;nttL=query(ls,l,M);tR=query(rs,M+1,r);nttans.sum=L.sum+R.sum;nttans.f=min(L.f,L.sum+R.f);nttreturn ans;nt}n}nvoid solve(){ntcin>>n>>m;ntcin>>s;ntfor(int i=0;i<n;i++) a[i+1]=(s[i]=='(')?1:-1;ntbuild(1,1,n);ntwhile(m--){nttint op,l,r;n cin>>op>>l>>r;nttif(op==1){ntttif(a[l]==a[r])tcontinue;ntttswap(a[l],a[r]);ntttupdate(1,l);tupdate(1,r);ntt}nttelse{nttttree tmp=query(1,l,r);ntttif(!tmp.sum&&!tmp.f)tcout<<"Yesn";ntttelsetcout<<"Non";ntt}nt}n}n

G - Vertex Deletion

给定一棵树，问有多少个节点满足：删去这个节点后的图的匹配数等于原树的匹配数。

首先：匹配数 = 节点数 - 最大独立集。

那么我们可以预处理出原树的匹配数。设 表示 子树中， 不选 / 选的最大独立集大小。

然后删去一个点后，新图的最大独立集大小是其他联通块的最大独立集大小之和，而 儿子的子树内最大独立集以求出，那么我们的目标就是要求出 子树外的最大独立集大小。

设 表示不考虑 子树， 的父亲不选 / 选的最大独立集大小。

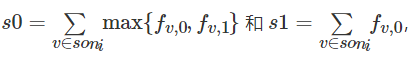
转移方程如下：

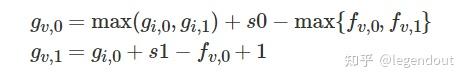
const int maxn=2e5+100;nint n,m,k;nint g[maxn][2], f[maxn][2];nvector<int>e[maxn];nvoid dfs(int u, int fa){ntf[u][1] = 1;ntfor (auto v : e[u]){nttif (v == fa) continue;nttdfs(v, u);nttf[u][0] += max(f[v][0], f[v][1]), f[u][1] += f[v][0];nt}n}n nvoid dfs1(int u, int fa){ntint s0 = 0, s1 = 0;ntfor (auto v : e[u]){nttif (v == fa) continue;ntts0 += max(f[v][0], f[v][1]), s1 += f[v][0];nt}ntfor (auto v:e[u]){nttif (v == fa) continue;nttg[v][0] = max(g[u][0], g[u][1]) + (s0 - max(f[v][0], f[v][1]));nttg[v][1] = g[u][0] + s1 - f[v][0] + 1;nttdfs1(v, u);nt}n}n nvoid solve(){ntcin>>n;ntfor (int i = 1; i < n; i+=1){nttint u,v;cin>>u>>v;ntte[u].pb(v);ntte[v].pb(u);nt}ntdfs(1, 0);ntint ans = n - max(f[1][0], f[1][1]), cnt = 0;ntdfs1(1, 0);ntfor (int i = 1; i <= n; i+=1){nttint bs = n - 1;nttint now = f[i][0] + max(g[i][0], g[i][1]);nttif (bs - now == ans) ++cnt;nt}ntcout<<cnt;n}n