俗话说，人往高处走，水往低处流。自古以来，人们就对高处的地方有着无穷的向往。对于物理学家来说，除了可以攀爬地理上山峰以外，也要不断

俗话说，

人往高处走，水往低处流。

自古以来，

人们就对高处的地方有着无穷的向往。

对于物理学家来说，

除了可以攀爬地理上山峰以外，

也要不断攀登科学的高峰，

这意味着需要不断创造更极限的实验环境。

Part I 又恐琼楼玉宇，高处不胜寒

众所周知，生活在平原或者低海拔地区的人在进入高原后，由于气压降低，氧气含量降低，同时可能受紫外线、气温低等因素影响容易出现高原反应。

但是你知道吗？除了人以外，我们平时所用的生活用品也会出现高反哟~

比如牙膏、洗面奶等物品会自己喷涌而出，薯片等膨化食品的袋子会膨胀地很大并爆开。

图片来源：微博

这些现象都是由于外界气压降低导致物体内部的气体与外界形成气压差而引起的。

所以，首先一个问题当然是为什么海拔越高，气压越低？

我们先考虑一定高度处的一小层薄薄的大气，它的厚度为dz。中学物理告诉我们，看到一个物体先对它干什么？

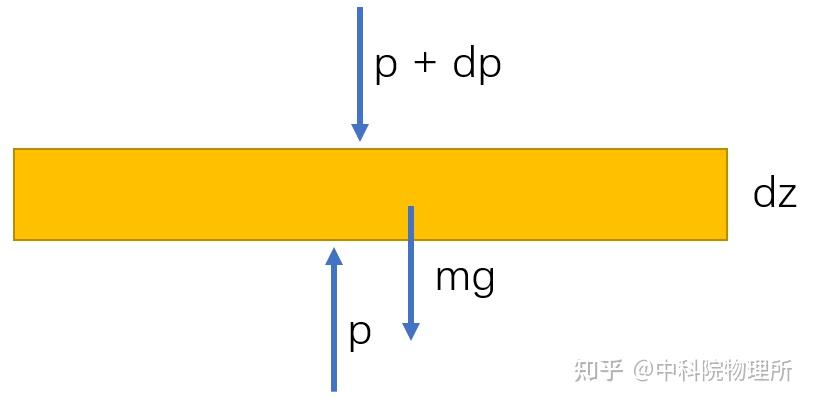
当然是先进行受力分析了！

这层大气受到自身的重力，上下表面气体的压力，我们可以假设下表面的压力为p，由于大气压随高度肯定是变化的，所以可以将上表面的气压设为p+dp。

根据受力平衡，可以有公式（其中A是气体柱的底面积，ρ(z)为大气密度）[1]：

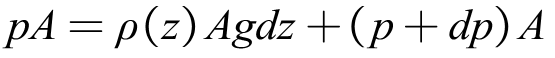
简化一下变成：

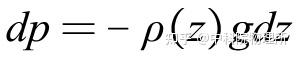
在这里我们可以先暂时假设大气的温度不随高度变化，虽然这个假设很粗糙，但是在海拔11-12km的位置可以认为是近似成立的[2]。

带入理想气体状态方程：pV=nRT，即：pM=ρ(z)RT，其中M为大气分子的摩尔质量。

并做积分即可得到大气压力p随海拔高度z的变化：

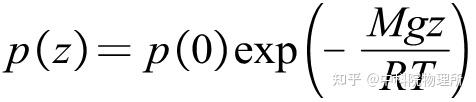
这个模型又被称为等温大气模型。

当然我们日常的感受是气温往往随着海拔高度升高而降低。

由于气压和温度变化关系非常复杂，所以我们可以采用多方状态过程来描述：

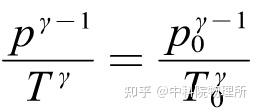
其中γ是大气的比热比，p和T0是地表的大气压强和温度。

代入上面的公式再积分可以得到更加精确地的大气压强p随海拔高度z的变化：

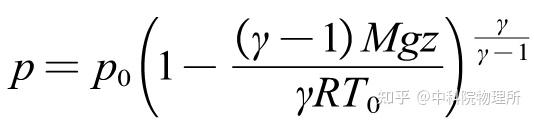
通过计算数值可以知道，当γ取1.235时得到的大气压随海拔高度的变化比较精确。

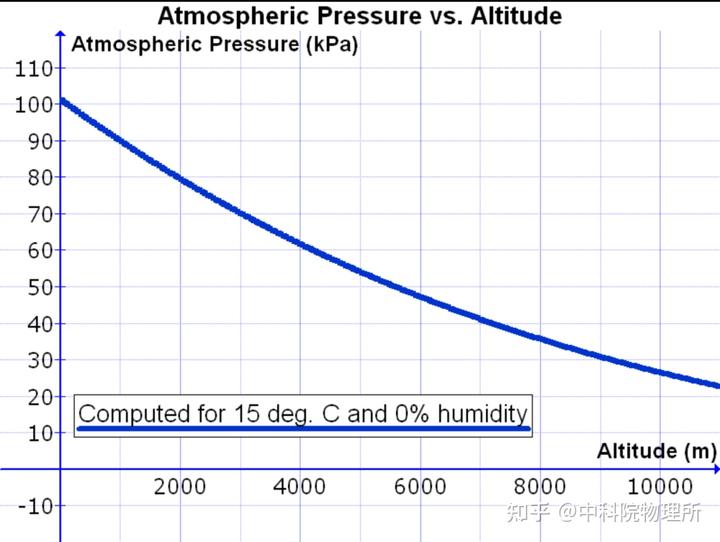
大气压强随海拔高度的变化曲线 (图源：Atmospheric pressure - Wikipedia)

Part II 欲穷千里目，更上一层楼

从上面的讨论我们可以知道，在高原地区，很多物体的“高反现象”来自于低气压。

换句话说，薯片和牙膏的膨胀都是来自于其本身内部相比外界有了一个相对“高”的压力。除此之外，大家也都知道在高原地区由于气压低导致水的沸点低，导致做饭做不熟，而高压锅就能解决这个问题。

除了我们日常生活中使用的高压锅以外，实际上，在实验室中，我们也可以通过一些手段制造一些高压环境，使各种材料处于高压之下，从而可以发现很多有趣的现象。

最简单的实现高压的方法就是对气体或者液体进行压缩，比如对于气体来说，根据前面所提的气体的状态方程：pV=nRT。

由此可以知道，等温压缩过程压缩气体的体积即可实现增大压力。

所以，最早的高压科学装置就是由英国物理学家Parsons在19世纪末期设计加工的活塞-圆筒装置。

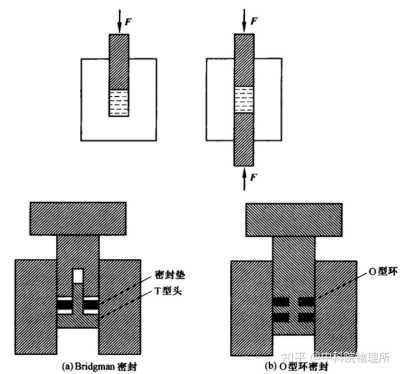
活塞-圆筒装置及密封方法示意图[3]

由于加压腔体体积很大，加上材料的限制，这个装置并不能加到很高的压力。现在往往用于产生5GPa以下的压力环境（约5万的大气压）。

现代活塞-圆筒装置实物图 图源：百度图片

随后在20世纪中期，美国物理学家Bridgman引入一个“压砧”（读作鸭胗）装置实现更高压力的实现，这个装置被称为Bridgman压机。

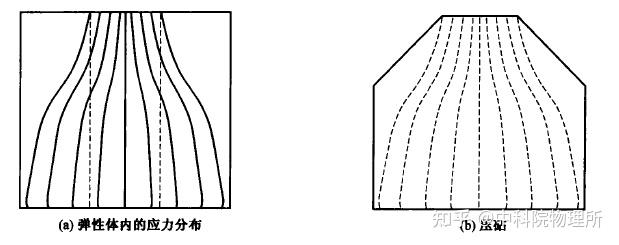
压砧示意图，弹性材料截掉边角后内部承压不发生变化[3]。

现代高压技术的基本构造还是以Bridgman压机为基础的。其原理就是用压砧支撑一个大质量材料，应力传到均匀的压砧表面实现均匀的压强分布。压砧材料一般为硬质合金。

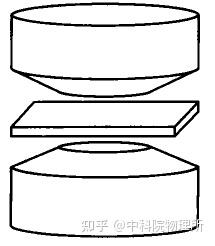
Bridgman压机[3]

由于活塞-圆筒装置的腔体大，导致极限压力低。压砧装置中样品薄，容易形变严重。

为了改善二者的缺点，Drickamar 和Balchan将压砧和圆筒进行组合，设计出Drickamar装置。由于对压砧的侧面也进行了支撑，所以可以极大的提高其极限压力。

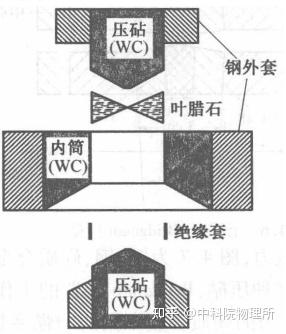
Drickamar装置[3]

为了在腔体中施加一个均匀的压力大小，人们又发展了多面体压砧，将高压腔体设计成为正多面体的形状，从而实现腔体内较为均匀的静压环境。

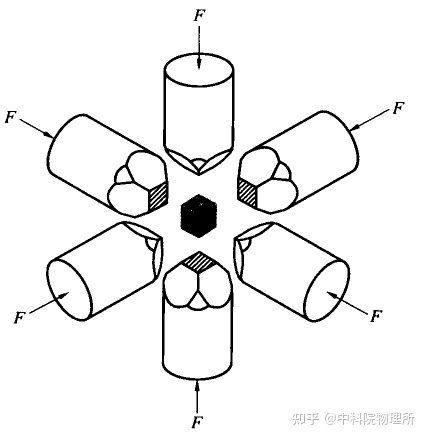
比如以正六面体腔体装置中的压砧配置[3]

众所周知，金刚石是已知的最硬的物质，那么用金刚石作为压砧材料必然可以实现极高的极限压力。这就是金刚石对顶砧。

利用金刚石对顶砧进行高压实验的原理非常简单：将样品放置在两个金刚石面的中间，然后挤压中间的密封材料而产生高压。密封材料的小孔内充满液态或固态的传压介质，使处于密封材料中的样品受到静水压或者准静水压。

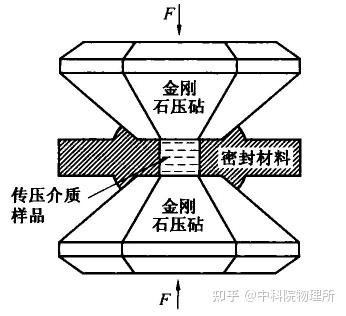
金刚石压腔原理图[3]

更细节地讲，一个金刚石压腔通常包含由下图中所示的腔主体(包括底座，活塞，带有增加压力和控制分离的螺丝的帽)、砧座、金刚石砧座和垫圈组成，其中金刚石结构和垫圈是最重要的部分。

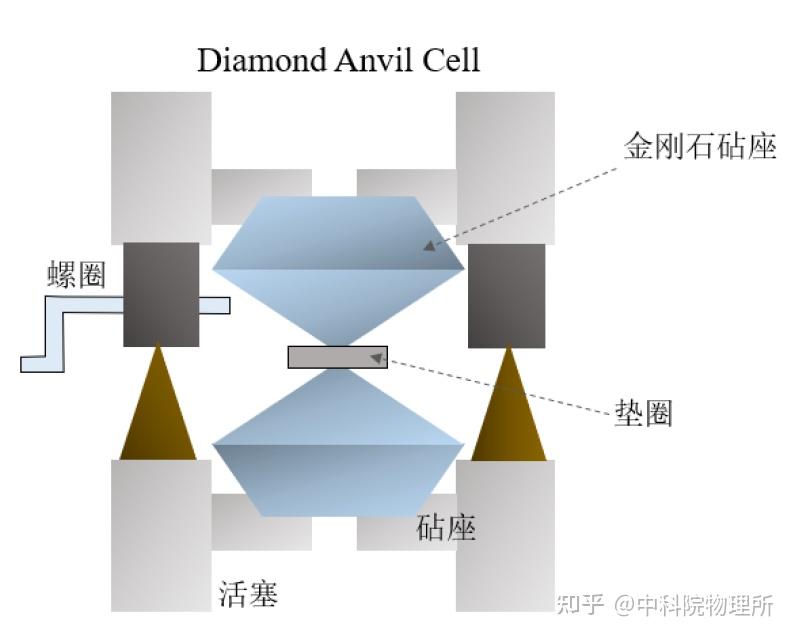
值得注意的是，由于金刚石质地非常脆，在加压时需要施加给金刚石巨大的力（约1万N），所以要避免两个金刚石直接接触，这要求极其精确的机械控制，控制精确须达到微米级[4]。

砧座往往由耐用的材料做成（比如碳化钨）以承受需要施加的巨大的力。垫圈是一块带孔的金属片，用于承载样品，它的作用在于更好地将样品控制在一个小的区域以保证施加在上的压力梯度是均匀的，同时可以保护金刚石不被直接接触导致断裂。

迄今为止，利用金刚石对顶砧已达到550GPa的高压（550万倍大气压）。

由于金刚石是透明材料，可以透过可见光、近红外光、x射线等电磁辐射，所以可以广泛地应用于高压科学之中。

金刚石对顶砧实物图[6]

在完成了高压的实现后，下面一步要考虑地则是如何对高压进行标定，也就是说，通过什么办法才能知道施加的压力数值是多少呢？

最可靠的测量超高压强的方法就是利用已知材料的状态方程。

一些简单结构的化合物在高压下的状态方程已经利用冲击波实验得到。但是这种方法最大的缺点是需要利用X射线测量，不容易实现[4]。

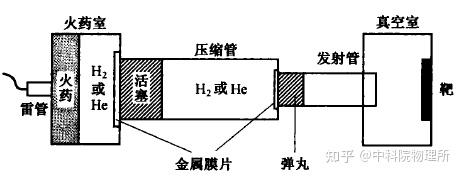
轻气泡产生平面冲击波示意图[3]

在金刚石压砧中，最常用的方法便是Forman等人第一次提出利用光谱的方法进行压力标定[5]。最常用的压力标定材料是红宝石。

红宝石的主要成分是掺杂Cr离子的氧化铝，其内部的Cr离子存在一系列的能级，电子在吸收一定能量的光后，会先跃迁到一个能量较高的能级，进而自发跃迁到另一个较低能量的能级，从而辐射出荧光。

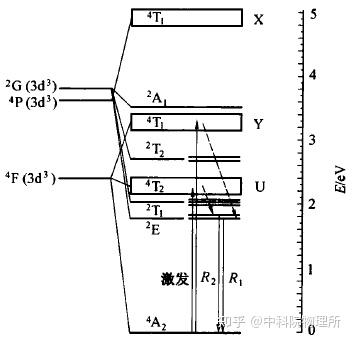
红宝石的电子能级结构[3]

辐射的荧光波长会随着压力的变化而变化。所以可以通过测定红宝石辐射荧光的波长而确定当前其所处的压力状态。

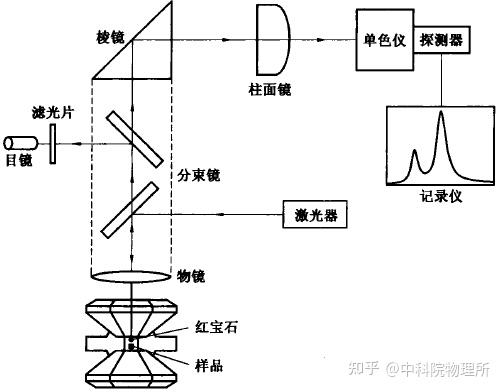
激光红宝石测压系统[3]

同时，红宝石可以被加工成微米大小并能产生良好的信号，所以，这一技术的实现极大地促进了高压实验技术的发展。

Part III 会当凌绝顶，一览众山小

当物质处于高压的环境时，它们也会表现出一些与在常压下不同的性质。我们可以称呼它们发生了高压反应（或简称高反）。

我们最常见的高压的作用应该就是高压锅了，高压锅可以让食物更容易熟透，比如将肉炖的更加软烂。这是因为在高压下，水的沸点升高了。水开时的温度更高，利用更高的温度烹饪食物当然事半功倍。

高压对物质的作用最直接的就是压缩了物体的体积，也就是使得物质内部原子之间的间距变小了。从而使气体变成液体，液体变成固体，固体的密度增大。

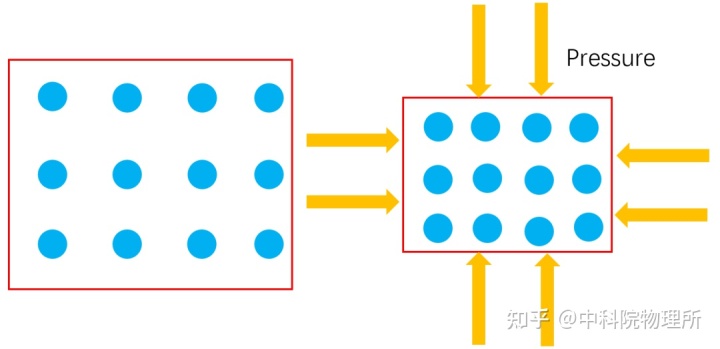
比如在更高的压力下，水不仅会变成冰，而且随着压力的不断升高，人们发现冰的性质也在发生变化。在0.2GPa下，水会形成在常压下不稳定的冰结构，这其实是一种新的冰结构。在更高的压力下，水还具有十几种不同的结构[3]。

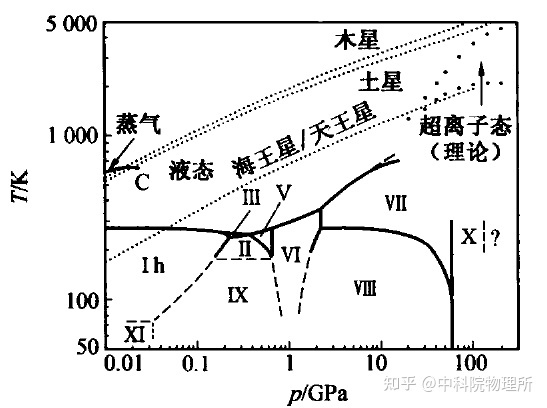
水的相图[3]

除此之外，原子间距的变化可能会引起原子排列的变化。

比如说某个原子可以和之前距离比较远的原子发生相互作用，从而增大配位数。或者原子间的相互作用发生改变，从而影响化学键的强度。也就是说压力引起了晶体的结构相变。比如在高温高压下石墨可以变成金刚石[6]。

更进一步地，由于原子间距的缩小，从而使得不同原子之间的能级更容易交叠，表现在晶体中就是压力导致了晶体能带发生改变。

对于半导体或者绝缘体来说，高压可以诱导导带和价带发生交叠，从而使半导体或绝缘体变成导体。

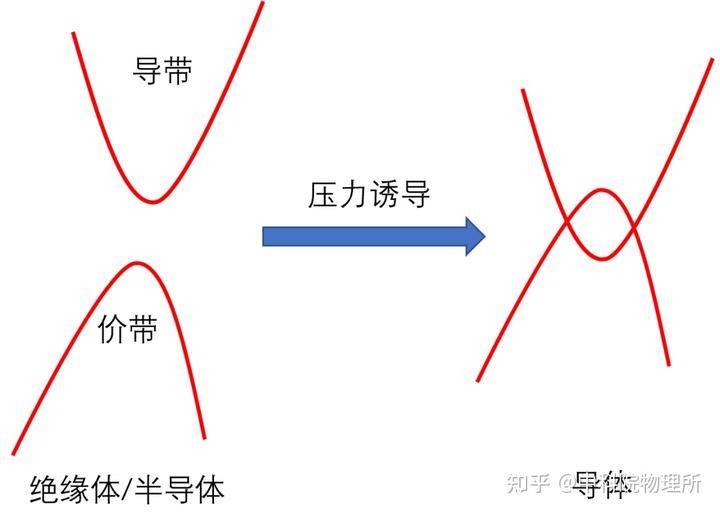
比如I在16GPa压力下发生从绝缘态到金属态的转变[6]。NaYbSe在50GPa压力下从绝缘体变成金属[7]。

如何实现高温超导被喻为凝聚态物理学皇冠上的明珠，高压科学为摘得这一明珠提供了手段。

在常规超导体的BCS理论中，超导体的转变温度与组成超导体的原子质量大致有一个平方根反比的关系：

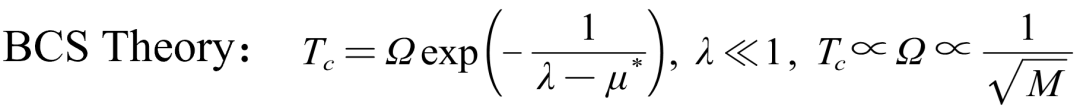
这意味着原子质量越小的元素组成的晶体越容易有更高的超导转变温度。

所以氢原子作为最轻的原子，如果可以制备出固态的氢，那么其或许就有很高的超导转变温度。

遗憾的是，即使在目前数百GPa（百万倍大气压力）的极高压力下，仍没有发现可以固化氢的可能性。但是退而求其次，科学家们制备出了富氢化合物：SH（203K）和LaH（250K），发现其具有很高的超导转变温度[4]。

除了常规超导体以外，在高压下，高温铜氧化物超导体的超导转变温度也可以提升。在1.4GPa下，镧钡铜氧体系的超导转变温度从35K提升到了52K。这启发了人们选用了原子半径更小的钇元素来代替镧元素，从而将超导转变温度提升到了93K。汞钡铜氧体系在高压下甚至能达到164K转变温度[3]。

高压高温超导体发展历程[4]

总之，超高压技术作为一种极端实验环境，是物理学家不断攀登科学高峰的体现。

超高压技术的实现也为研究新材料、发现新物理开拓了一个广泛的天地。

参考文献：

[1] 秦允豪，热学. 高等教育出版社，2011年 第三版

[2] 吕岿，王霞，用改进的基因算法求大气压强公式. 大学物理，2004年底23卷第3期

[3] 刘志国，千正男，高压技术. 哈尔滨工业大学出版社，2012年

[4] J. A. Flores-Livas, M. Eremets etc. A perspective on conventional high-temperature superconductors at high pressure: Methods and materials, Phys. Rep. 856, 1 (2020)

[5] Forman RA, Piermarini GJ, Dean Barnett J, Block S. Pressure measurement made by the utilization of ruby sharp-line luminescence. Science. 1972;176(4032):284-5.

[6] 郭思洋, 高压下二氧化碳和二氧化硅的相变与弹性性质研究. 吉林大学博士论文，2021年

[7] Ya-Ting Jia etc. Mott Transition and Superconductivity in Quantum Spin Liquid Candidate NaYbSe2. Chin.Phys.Lett, 37, 097404 (2020)

编辑：Garrett